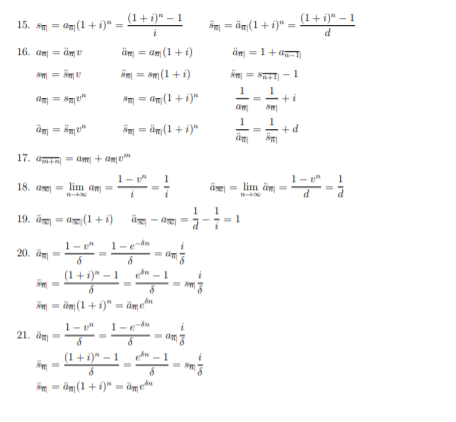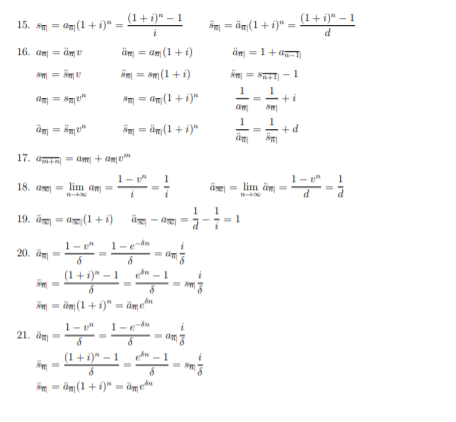
Calculate the present value of annuity with payment of $1 at the end of the first year and every two years thereafter. There are total 5 payments. The last payment of $1 is at the end of 9th year. The interest rate is 6% convertible semi-annually. The present value of perpetuity of $600 paid at the end of each year plus the present value of a perpetuity of $800 paid at the end of every 5 years is equal to the present value of an annuity of k paid at the end of each year for 25 years. Interest is 6% convertible quarterly. Calculate k. At) - Alt - 1) a(t)-at-1) amount earned Alt - 1) alt - 1) beginning amount . For simple interest: a(t) = 1 +it A(t) = (1 + it), where i is the simple interest rate (1 + it) - (1+it - 1) i 1+it - 1)) 1+ift - 1) . For compound interest: a(t) = (1 + i)' (t) - k(1+1), where i is the compound interest rate (1 + i)' - (1 + i)(-1) (1 + i)(-1)(1+1-1) (1 + i)t - 1) (1 + i)(-+) 2. a(t) = 1 + it A(t) = A(0)(1 + it) 3. a(t) = (1 + i)' A(t) = A(0)(1 + i) 4. PV = FV(1 + i) = FV v' = FV(1 - d)" 5. FV = PV(1 + i)' = PVv4 = PV(1 - 1) d 6. d = iu d=1- U=l-d 1- 7. (1+ 1+ (1+ -= (1 - m m P 8. limm, lim dm) 8 At) d 9. A(0) ale) - llna(t) - IAC) 10. a(t) = 11. aft) -(1+1) 12. 1+1=(1+ - (1 - - - 13. : -In(1+i) 1- 1 1 - im = m(1+i) HH 1 whered 15. mm (1 + i)" (1 + i)" - 1 = m (1 + i)" (1+i)" - 1 d n = 1+ = 16. cm = n = m (1 + i) m = (1 + i) = (1+i)" 1 1 1 1 mi mu" m = (1 + i)" +d 17. m + 1 1 18. lim a = limi 1 19. 4, (1 + i) -421 11 1- 1-- 20. Um 8 1 (1 + i)" - 1 3min (11)" =me 1 - - 1 21. am (1 + i)" - 1 6 m = (1+1)" = Omer Calculate the present value of annuity with payment of $1 at the end of the first year and every two years thereafter. There are total 5 payments. The last payment of $1 is at the end of 9th year. The interest rate is 6% convertible semi-annually. The present value of perpetuity of $600 paid at the end of each year plus the present value of a perpetuity of $800 paid at the end of every 5 years is equal to the present value of an annuity of k paid at the end of each year for 25 years. Interest is 6% convertible quarterly. Calculate k. At) - Alt - 1) a(t)-at-1) amount earned Alt - 1) alt - 1) beginning amount . For simple interest: a(t) = 1 +it A(t) = (1 + it), where i is the simple interest rate (1 + it) - (1+it - 1) i 1+it - 1)) 1+ift - 1) . For compound interest: a(t) = (1 + i)' (t) - k(1+1), where i is the compound interest rate (1 + i)' - (1 + i)(-1) (1 + i)(-1)(1+1-1) (1 + i)t - 1) (1 + i)(-+) 2. a(t) = 1 + it A(t) = A(0)(1 + it) 3. a(t) = (1 + i)' A(t) = A(0)(1 + i) 4. PV = FV(1 + i) = FV v' = FV(1 - d)" 5. FV = PV(1 + i)' = PVv4 = PV(1 - 1) d 6. d = iu d=1- U=l-d 1- 7. (1+ 1+ (1+ -= (1 - m m P 8. limm, lim dm) 8 At) d 9. A(0) ale) - llna(t) - IAC) 10. a(t) = 11. aft) -(1+1) 12. 1+1=(1+ - (1 - - - 13. : -In(1+i) 1- 1 1 - im = m(1+i) HH 1 whered 15. mm (1 + i)" (1 + i)" - 1 = m (1 + i)" (1+i)" - 1 d n = 1+ = 16. cm = n = m (1 + i) m = (1 + i) = (1+i)" 1 1 1 1 mi mu" m = (1 + i)" +d 17. m + 1 1 18. lim a = limi 1 19. 4, (1 + i) -421 11 1- 1-- 20. Um 8 1 (1 + i)" - 1 3min (11)" =me 1 - - 1 21. am (1 + i)" - 1 6 m = (1+1)" = Omer