(Calculating ) In this problem you will calculate to an accuracy of 1/100 by using the...

(Calculating π) In this problem you will calculate π to an accuracy of 1/100 by using the formula of Machin. We will use in this problem that arctan is a infinitely differentiable function and that arctan(1) = π/4, and that the derivative of arctan(x) is 1/(1 + x²). These things were discussed in class. After the statements of the individual parts is a list of hints to consider in case you get stuck. You shouldn’t need a calculator except possibly for the last part where you plug in.

Angle addition formula for tangent:

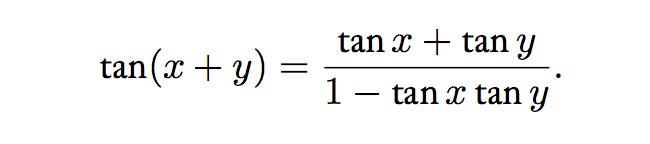 Using the previous formula we deduce the following relationship concerning arctan:

 And using the previously derived relationship concerning arctan we showed that

 The second identity above is known as “Machin’s Formula.”
(d) Let P be the Taylor polynomial of order 3 for arctan centered at 0. We showed that

 

(if you need the previous workings for above parts, please ask for more information)

a)Show, using the previous part, that

 

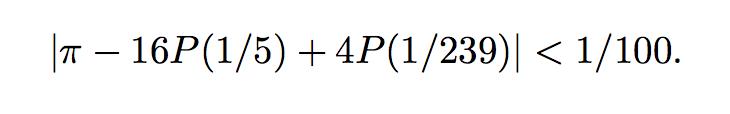
b)Now Compute P , the Taylor polynomial of order 3 for arctan centered at 0.

c)Using everything you have done so far, obtain an approximation for π that is within 1/100 of the true value.

Transcribed Image Text:

tan(x + y) tan x + tan y 1 - tan x tan y tan(x + y) tan x + tan y 1 - tan x tan y

Answer rating: 100% (QA)

To calculate to an accuracy of 1100 using Machins formula we need to complete the steps a b and c as outlined a We are to show the given formulas deri... View the full answer