Question: Calculus 3: Section 11.6: Problem 11 [1 point} Consider the surface a: 2 55:2 + 332 1?8. Find an equation of the tangent plane to


![rft] = E]. Section 11.6: Problem 12 [1 point} Consider the surface](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66672a481ec47_06466672a480b25a.jpg)

![to this surface at ( Hi, i], 1}]. E] Find a 1"rector](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66672a48de7a2_06466672a48cd850.jpg)
![equation for the normal line to the surface at [10, i], D}.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66672a4934988_06566672a4921140.jpg)
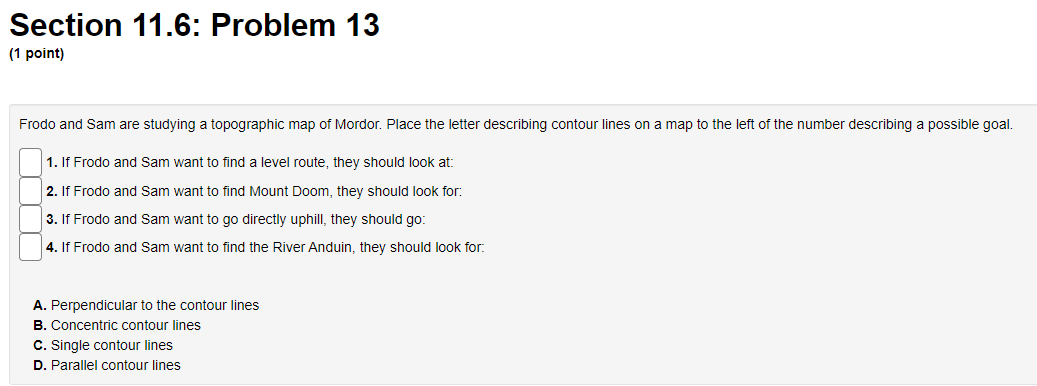
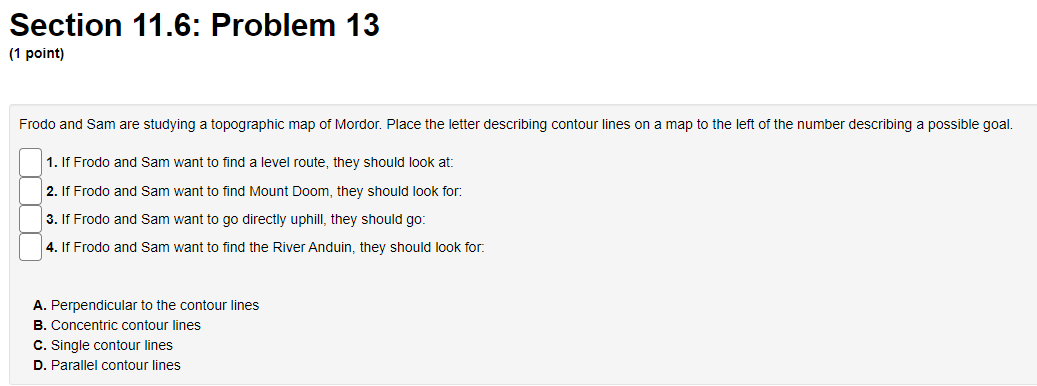
![rft] = E] Section 11.6: Problem 13 (1 point) Frodo and Sam](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66672a49822ec_06566672a49682e4.jpg)

Calculus 3:


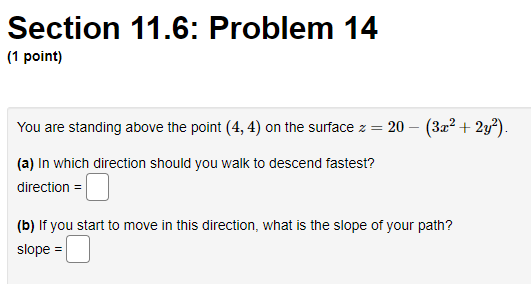


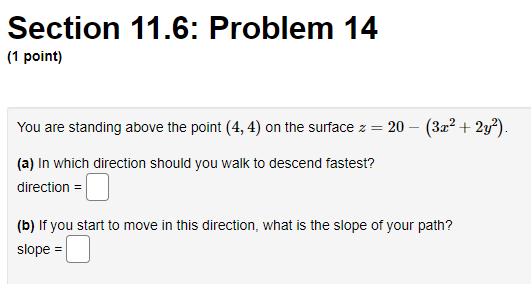
![standing above the point {4, 4] on the surface s = 21]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66672a4ce04d5_06866672a4cd0b73.jpg)
![{322 + 23?]. {a} In which direction should you walk to descend](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66672a4d3f4c1_06966672a4d219ec.jpg)
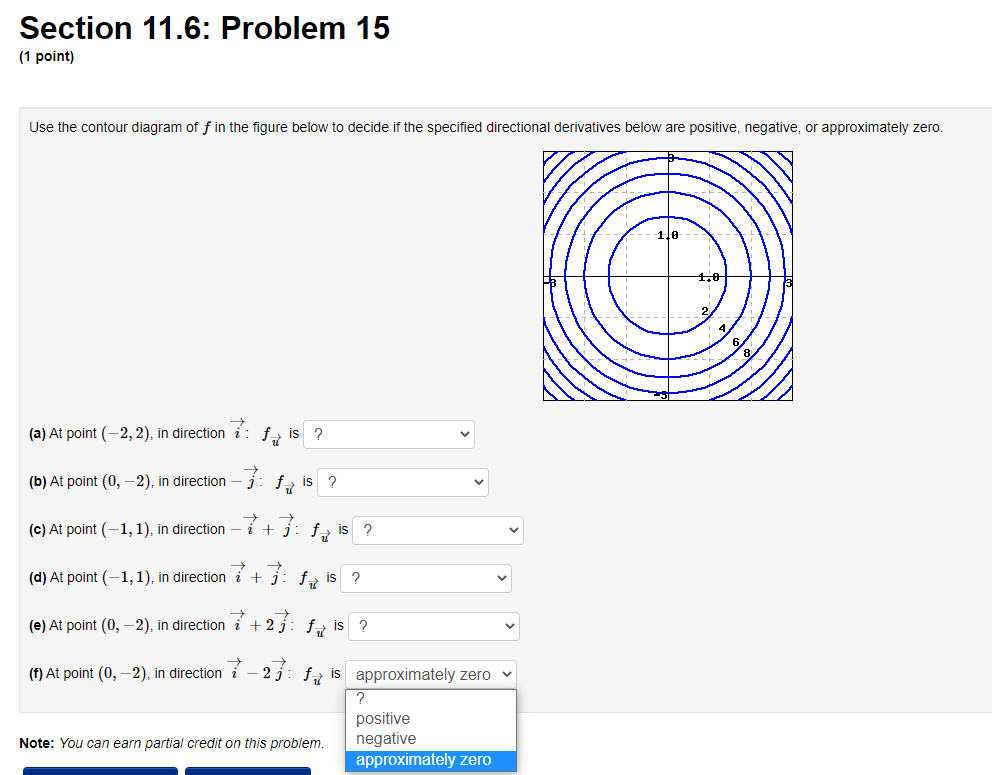
Section 11.6: Problem 11 [1 point} Consider the surface a: 2 55:2 + 332 1?8. Find an equation of the tangent plane to the surface at the point {11.1, 4, ). Find a 1"rector equation of the normal line to the surface at {1,4, } rft] = E]. Section 11.6: Problem 12 [1 point} Consider the surface 3 ID = rev-sous 2:. Find an equation of the tangent plane to this surface at ( Hi, i], 1}]. E] Find a 1"rector equation for the normal line to the surface at [10, i], D}. rft] = E] Section 11.6: Problem 13 (1 point) Frodo and Sam are studying a topographic map of Mordor. Place the letter describing contour lines on a map to the left of the number describing a possible goal. 1. If Frodo and Sam want to find a level route, they should look at: 2. If Frodo and Sam want to find Mount Doom, they should look for: 3. If Frodo and Sam want to go directly uphill, they should go: 4. If Frodo and Sam want to find the River Anduin, they should look for. A. Perpendicular to the contour lines B. Concentric contour lines C. Single contour lines D. Parallel contour linesSection 11.6: Problem 14 [1 point} You are standing above the point {4, 4] on the surface s = 21] {322 + 23?]. {a} In which direction should you walk to descend fastest? direction = E] [b] If you start to moye in this direction, what is the slope of your path? slope =E] Section 11.6: Problem 15 (1 point) Use the contour diagram of f in the figure below to decide if the specified directional derivatives below are positive, negative, or approximately zero. (a) At point (-2, 2), in direction i : f is ? (b) At point (0, -2), in direction - j : f is ? (c) At point (-1, 1), in direction - i + j : f is ? (d) At point (-1, 1), in direction i + j : for is ? (e) At point (0, -2), in direction i + 2 j : fo is ? (f) At point (0, -2), in direction i - 2 j : f is approximately zero positive Note: You can earn partial credit on this problem. negative approximately zeroSection 11.6: Problem 16 [1 point} A car is driving northwest at 1.- mph across a sloping plain whose height, in feet above sea level, at a point N miles north and E miles east of a city is given by MN, E) = 4750 + 251v + 'i'E. {a} At what rate is the height above sea level changing with respect to distance in the direction the car is driving? m {1 [b] Express the rate of change of the height of the car with respect to time in terms of u. rate=D Section 11.6: Problem 17 [1 point) You are climbing a mountain by the steepest route at a slope of 20 when you come upon a trail branching off at a 45 angle from yours. What is the angle of ascent of the branch trail? angle = E] (in degrees) Section 11.6: Problem 18 (1 point) 140 The temperature at any point in the plane is given by T(x, y) =- x2+ +1 (a) What shape are the level curves of T? O A. hyperbolas OB. circles O C. parabolas OD. lines O E. ellipses OF. none of the above (b) At what point on the plane is it hottest? What is the maximum temperature? (c) Find the direction of the greatest increase in temperature at the point (-1, -3). What is the value of this maximum rate of change, that is, the maximum value of the directional derivative at (-1, -3)? (d) Find the direction of the greatest decrease in temperature at the point (-1, -3). What is the value of this most negative rate of change, that is, the minimum value of the directional derivative at (-1, -3)?Section 11.6: Problem 19 (1 point) At a certain point on a heated metal plate, the greatest rate of temperature increase, 6 degrees Celsius per meter, is toward the northeast. If an object at this point moves directly north, at what rate is the temperature increasing? degrees Celsius per meterSection 11.6: Problem 20 [1 point] Use the contour diagram for x, 3;) shown below to estimate the directional derivative of f in the direction it at the point P. (a) At the point P = (2, 2] in the direction it = 3, the directional derivative is approximately E] (ii) At the point P = (3, 2] in the direction it = ', the directional derivative is approximately C] (1:) At the point P = (1,4) in the direction it = (it + ELK/i the directional derivative is approximately C] (d)At the point P = (U, D] in the direction it = ', the directional derivative is approximately C] (Click on graph to enlarge)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


