Calculus
Answer these 5 problems, please.
( final result only is okay )
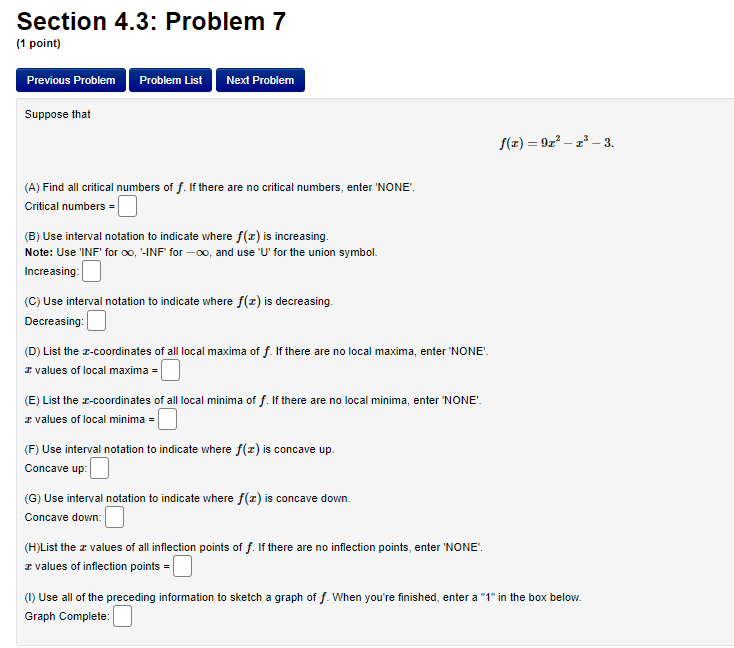
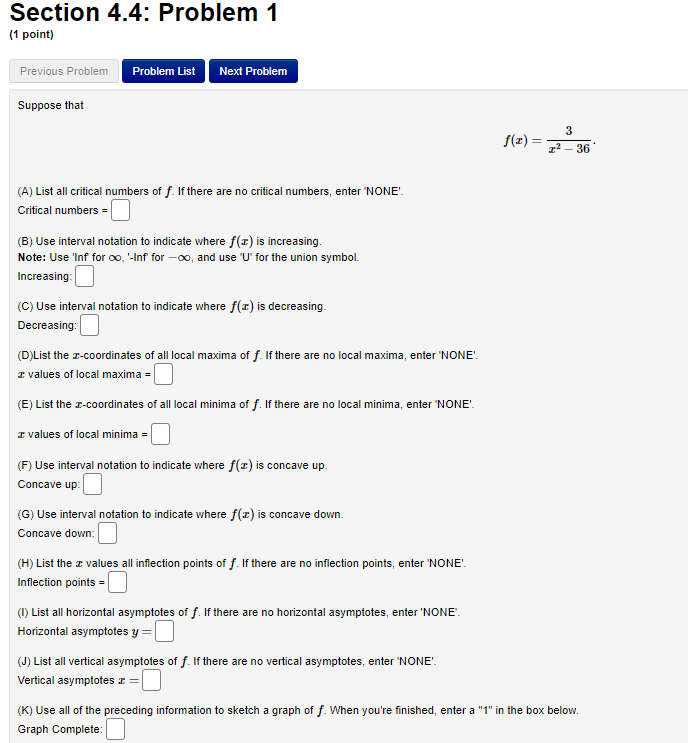
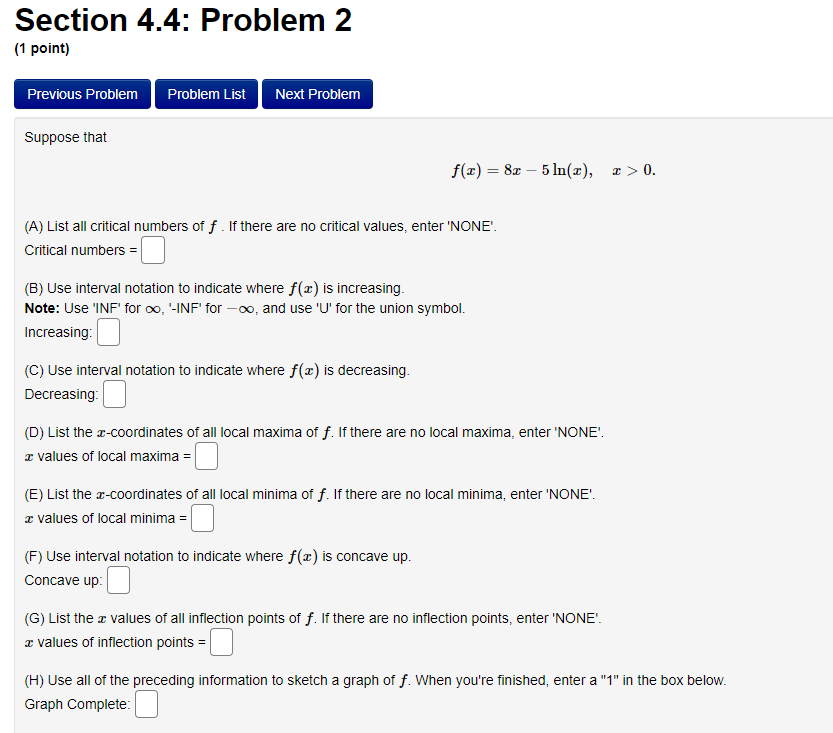
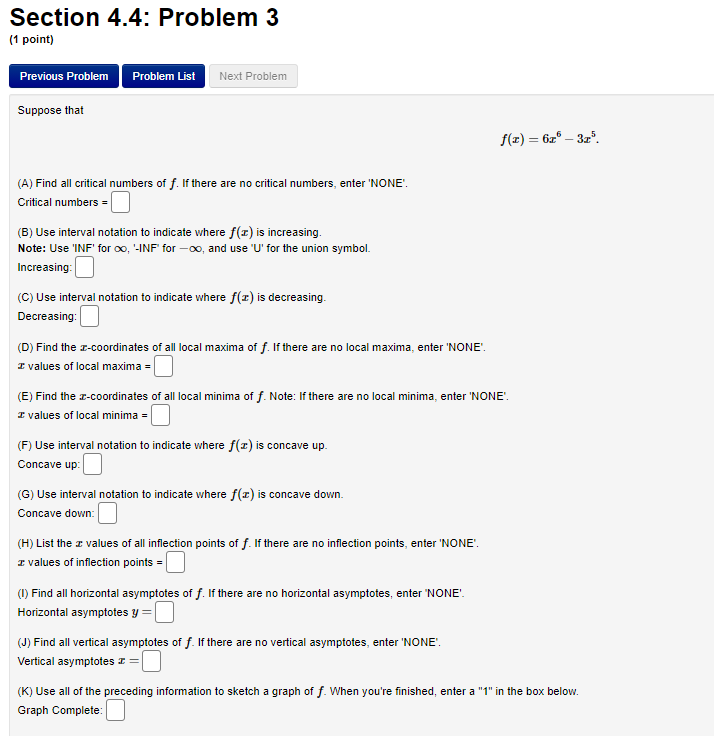
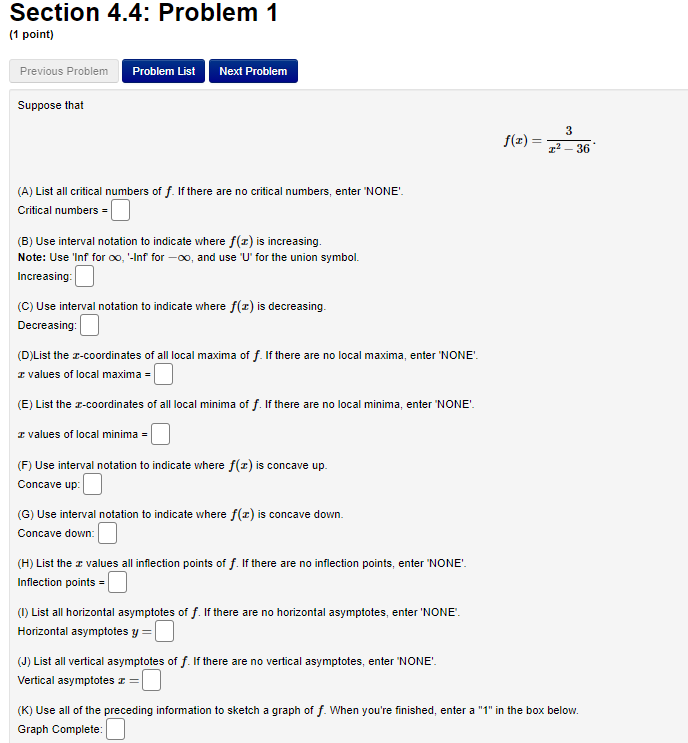
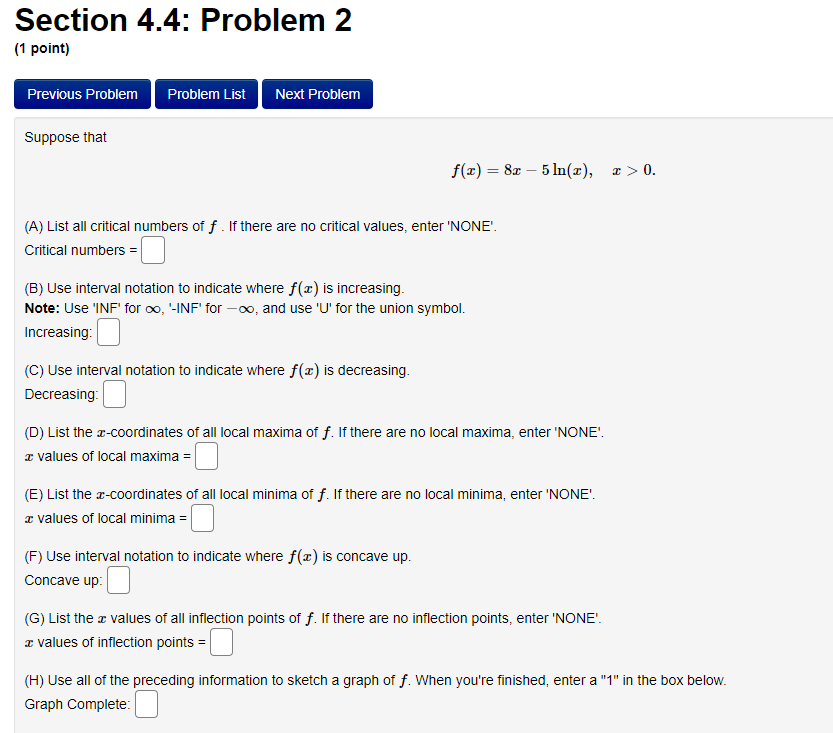
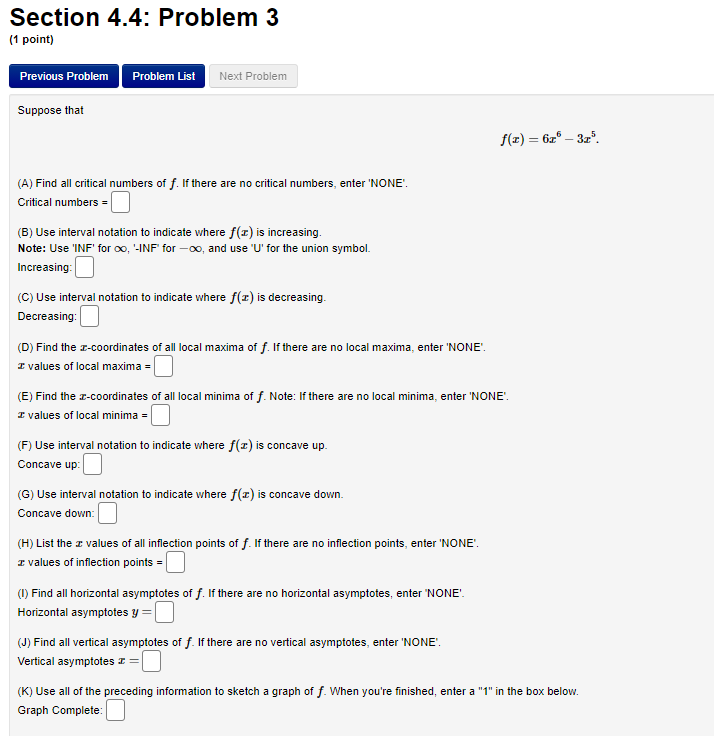
Section 4.3: Problem 7 (1 point) Previous Problem Problem List Next Problem Suppose that f(x) = 913 - 13 - 3. (A) Find all critical numbers of f. If there are no critical numbers, enter "NONE". Critical numbers = B) Use interval notation to indicate where f(I) is increasing. Note: Use 'INF' for oo, '-INF for -oo, and use "U' for the union symbol. Increasing: (C) Use interval notation to indicate where f(I) is decreasing. Decreasing: (D) List the z-coordinates of all local maxima of f. If there are no local maxima, enter "NONE' I values of local maxima = (E) List the r-coordinates of all local minima of f. If there are no local minima, enter "NONE' I values of local minima =| (F) Use interval notation to indicate where f() is concave up. Concave up: (G) Use interval notation to indicate where f() is concave down. Concave down: (H)List the c values of all inflection points of f. If there are no inflection points, enter 'NONE'. I values of inflection points = (I) Use all of the preceding information to sketch a graph of f. When you're finished, enter a "1" in the box below. Graph Complete:Section 4.3: Problem 8 (1 point) Previous Problem Problem List Next Problem Answer the following True-False quiz. (Enter "T" or "F".) 1. Continuous functions are differentiable. 2. A continuous function on a closed interval [a, b] attains a maximum and a minimum value in a, b]. 3. If a function has a local maximum at c, then f (c) exists and is equal to 0. 4. (f(x) + g(x))' = f'(x) + g'(x). 5. Differentiable functions are continuous. 6. If f'(c) = 0, then f has either a local maximum or a local minimum at c. 7. If f() and g(@) are increasing on an interval I, then f(x) g(x) is increasing on I.Section 4.4: Problem 1 (1 point) Previous Problem Problem List Next Problem Suppose that 3 f ( I) = - 12 - 36 (A) List all critical numbers of f. If there are no critical numbers, enter "NONE' Critical numbers = 6) Use interval notation to indicate where f (I) is increasing. Note: Use 'Inf for oo, '-Inf for -oo, and use "U" for the union symbol. Increasing: C) Use interval notation to indicate where f (I) is decreasing. Decreasing: (D)List the r-coordinates of all local maxima of f. If there are no local maxima, enter "NONE'. I values of local maxima =| (E) List the I-coordinates of all local minima of f. If there are no local minima, enter "NONE'. I values of local minima = (F) Use interval notation to indicate where f() is concave up. Concave up: (G) Use interval notation to indicate where f (I) is concave down. Concave down: (H) List the c values all inflection points of f. If there are no inflection points, enter "NONE' Inflection points = (1) List all horizontal asymptotes of f. If there are no horizontal asymptotes, enter 'NONE Horizontal asymptotes y = (J) List all vertical asymptotes of f. If there are no vertical asymptotes, enter "NONE' Vertical asymptotes = = (K) Use all of the preceding information to sketch a graph of f. When you're finished, enter a "1" in the box below. Graph Complete:Section 4.4: Problem 2 (1 point) Previous Problem Problem List Next Problem Suppose that f(x) = 8x - 5In(x), x >0. (A) List all critical numbers of f . If there are no critical values, enter 'NONE'. Critical numbers = (B) Use interval notation to indicate where f (x) is increasing. Note: Use 'INF' for co, "-INF' for -co, and use 'U' for the union symbol. Increasing: (C) Use interval notation to indicate where f(I) is decreasing. Decreasing: (D) List the x-coordinates of all local maxima of f. If there are no local maxima, enter 'NONE". I values of local maxima = (E) List the x-coordinates of all local minima of f. If there are no local minima, enter 'NONE'. I values of local minima = (F) Use interval notation to indicate where f(x) is concave up. Concave up: (G) List the x values of all inflection points of f. If there are no inflection points, enter 'NONE'. I values of inflection points = (H) Use all of the preceding information to sketch a graph of f. When you're finished, enter a "1" in the box below. Graph Complete:Section 4.4: Problem 3 (1 point) Previous Problem Problem List Next Problem Suppose that f(x) = 616 - 315. (A) Find all critical numbers of f. If there are no critical numbers, enter 'NONE'. Critical numbers = (B) Use interval notation to indicate where f(I) is increasing. Note: Use 'INF' for oo, '-INF for -oo, and use "U' for the union symbol. Increasing: (C) Use interval notation to indicate where f (I) is decreasing. Decreasing: (D) Find the r-coordinates of all local maxima of f. If there are no local maxima, enter 'NONE". I values of local maxima = (E) Find the I-coordinates of all local minima of f. Note: If there are no local minima, enter 'NONE" I values of local minima = (F) Use interval notation to indicate where f() is concave up. Concave up: (G) Use interval notation to indicate where f(I) is concave down. Concave down: (H) List the x values of all inflection points of f. If there are no inflection points, enter "NONE'. I values of inflection points = (1) Find all horizontal asymptotes of f. If there are no horizontal asymptotes, enter "NONE' Horizontal asymptotes y = (J) Find all vertical asymptotes of f. If there are no vertical asymptotes, enter "NONE'. Vertical asymptotes I = (K) Use all of the preceding information to sketch a graph of f. When you're finished, enter a "1" in the box below. Graph Complete