Calculus Based Physics 3 Chapter 41 Quantum Mechanics 2 Question 4

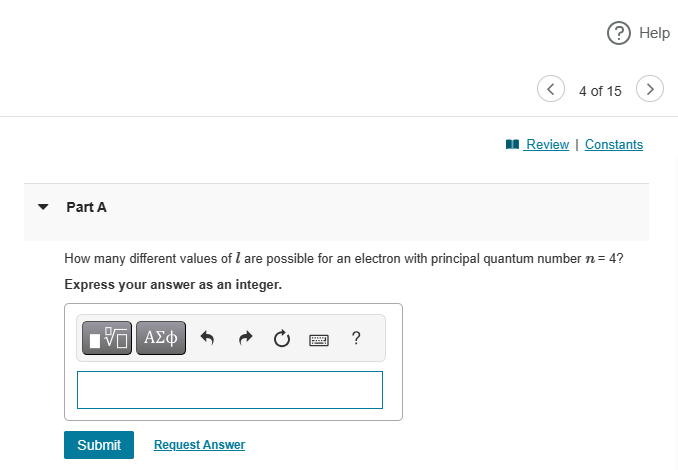
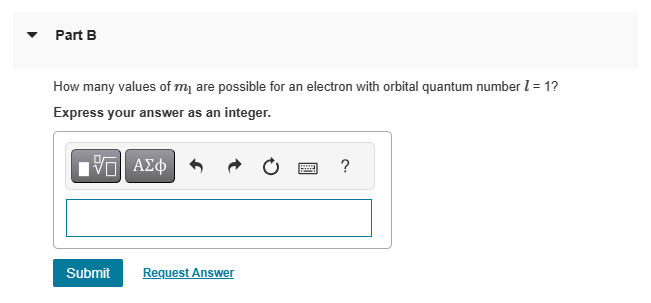
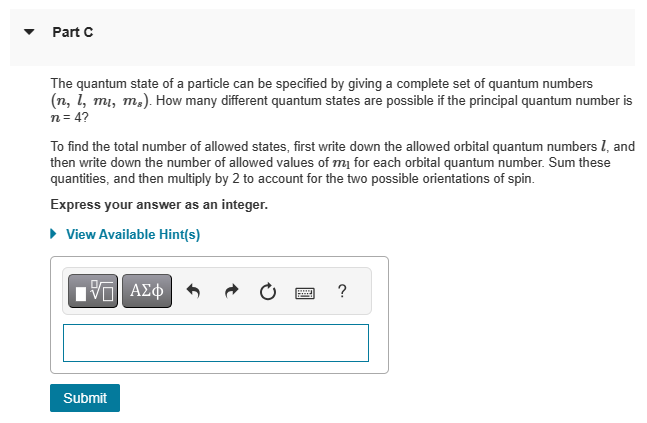
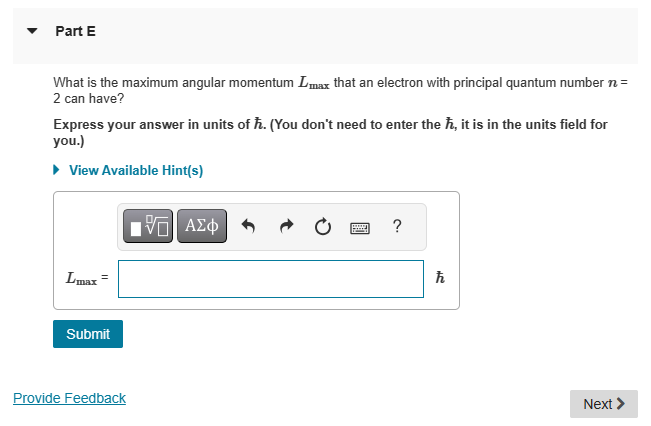
{HW 11 - Chapter 41 Rules for Orbital Angular Momentum Learning Goal: To understand and be able to use the rules for determining allowable orbital angular momentum states. Several numbers are necessary to describe the states available to an electron in the hydrogen atom. The principal quantum number 7 determines the energy of the electron. The orbital quantum number I determines the total angular momentum of the electron, and the magnetic quantum number determines the component of the angular momentum parallel to a specific axis, usually the z axis. For a given principal quantum number 7, the orbital guantum number can take integer values ranging from zero tom 1. For a given orbital quantum number I, the magnetic quantum number can take integer values from I to I. A fourth number, the spin M. is important for interactions with magnetic fields and counting states. The spin can be either |1 /2 or 1/2, independent of the values of the other guantum numbers. The energy of an electron in hydrogen is related to the principal quantum number by B (13.60 a"ui'}fnj . The orbital angular momentum is related to the orbital quantum number by I, h\\fm and the orbital angular momentum in the z direction is related to the magnetic quantum number by L. myh. @ Help 0= - v PartD Is the staten = 3,1 = 3, my = 2, m; = 1/2 an allowable state? If not, why not? ) Yesitis an allowable state. ) No: The magnetic quantum number must equal the orbital guantum number. ) No: The magnetic guantum number must equal the principal quantum number. ) No: The magnetic guantum number cannot be negative. ) No: The orbital quantum number cannot equal the principal quantum number. m Request Answer PartE What is the maximum angular momentum L., that an electron with principal quantum number n = 2 can have? Express your answer in units of k. (You don't need to enter the h, it is in the units field for you.) View Available Hint(s) 'ho Provide Feedback Next