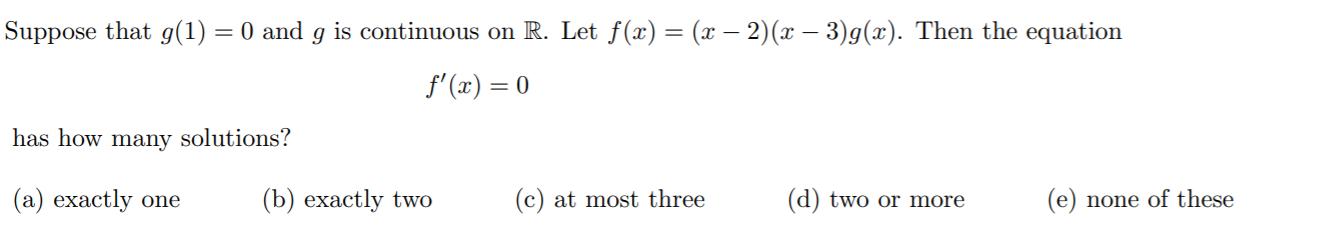Question: Suppose that g(1) = 0 and g is continuous on R. Let f(x) = (x 2)(x 3)g(x). Then the equation f' (x) = 0

Suppose that g(1) = 0 and g is continuous on R. Let

Suppose that g(1) = 0 and g is continuous on R. Let f(x) = (x 2)(x 3)g(x). Then the equation f' (x) = 0 has how many solutions? (a) exactly one (b) exactly two (c) at most three (d) two or more (e) none of these

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Suppose that f : R R is continuous and periodic. The modulus of continuity of f is defined by a) Show that for k N. b) Prove that for k N. c) Use part b) to give a different proof the...

Suppose that f : R R is continuous on R and that = 0 and Prove that f is bounded on R and attains either a maximum or minimum on R. Give an example to show that both a maximum and a minimum need not...

Suppose that c X and that f : E Y. a) Prove that f is continuous on E if and only if f-l (A) n is relatively closed in for all closed sets A in Y. b) Suppose that f is continuous on E. Prove that...

Suppose that x0 (-1, 0) and xn = xn-1 + 1 - 1 for n N. Prove that xn 0 as n . What happens when x0 [- 1, 0]?

Social entrepreneurs are entrepreneurs who use their talents to advance social causes that are typically linked to the provision of some type of public good. Their challenge within the civil society...

Suppose that f(z0) = g(z0) = 0 and that f'(z0) and g'(z0) exist, where g'(z0) 0. Use definition (1), Sec. 19, of derivative to show that f(z) f'(zo) g() g lim

3.3. Suppose that f,, ,, ... are independent and identically distributed with Pr(6R = 11 = ;. Let N be independent of 6, ,2, ... and follow the geometric probability mass function p,,(k) = all - a)'...

In the notation of Section 3.2, consider the problem of testing H0 : P = P0 against H1 : P = P1, and suppose that known probabilities 0 = and 1 = 1 can be assigned to H0 and H1 prior to the...

Figure shows a pendulum of length L with a bob of mass M. The bob is attached to a spring of spring constant k as shown. When the bob is directly below the pendulum support, the spring is at its...

1. Write a brief memo to Tammy explaining the importance of data validation during the input process. 2. Suggest at least three specific data validation checks that might help reduce input errors. 3....

Currently a put contract with an exercise price of $5 on a share of Mily be Aerospaces common stock is selling for (that is, its premium is) $1. What would the profit or loss graph (similar to...

The marketing department of a company is planning to launch a new product. They need to estimate the first-year net profit from this product, which depends on several factors, including sales volume,...

4 . Provide a comprehensive overview of the enrollment and premium revenues within the U . S . health insurance industry in 2 0 2 0 , as detailed in the annual report. Your answer should address the...

Explain the purpose of the following audit procedures: a. Sending a bank confirmation to all the banks with which the company does business. b. Obtaining a bank cutoff statement. c. Preparing a bank...

Suzuki Supply reports the following amounts at the end of 2015 (before adjustment). Credit Sales for 2015.................. $260,000 Accounts Receivable, December 31, 2015............. 55,000...

Match each of the following objectives to the relevant control activities. Objectives That Controls Are Trying to Achieve a. Payments received are deposited intact on a timely basis. b. Payments...

Match the following assertions with their associated description: (a) Existence or occurrence, (b) Completeness, (c) Rights and obligations, (d) Valuation or allocation, (e) Presentation and...

Minor Inc. sells 10% bonds having a maturity value of $3 million for $2,783,713. The bonds are dated January 1, 2017 and mature on January 1, 2022. Interest is payable annually on January 1....

Part B - Calculate the work done by the normal force, and the work done by gravity. Review on how to apply the work formula and identify the angle "" correctly. Open "hints" if you need

Let be a continuous real-valued function on the unit circle {x R2 : |x| =1} such that f (0, 1) = g(1, 0) = 0 and g(- x )= - g(x). Define f: R2R by F (x) = {|x| . g (x/|x| x 0, 0 x = 0. (a) If x R2...

8. Proportional income tax in simple dynamic model with a government and specific utility functions Consider the following economy: Time: Discrete; infinite horizon Demography: Continuum of mass 1 of...

Section 14.7: Problem 6 (1 point) Find all absolute extrema of each function. Enter each point as an ordered pair. e.g., "(1.5)". If an extreme value is attained twice, enter a commaseparated list of...

1. Human Capital in the SolowSwan Model: Suppose that the production function in the BelowSwan model is given by ya) = AK{t)QH(t)AL[t)1_'1_A where Y is output1 A is technology, K is physical capital,...

The one to one functions g and h are defined as follows g x 2x 3 h 8 5 7 4 4 8 3 0 Find the following g t 0 g g 1 0 h 8 3 X

*6. Suppose that ak 1 0 as k ---- 00. Prove that 00 L ak sin((2k + l)x) k=l converges for all x E R.