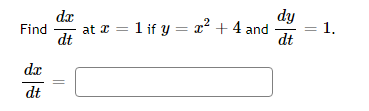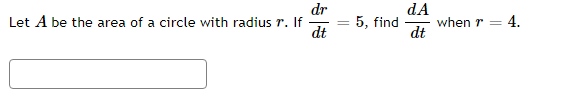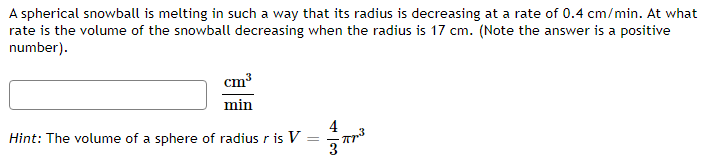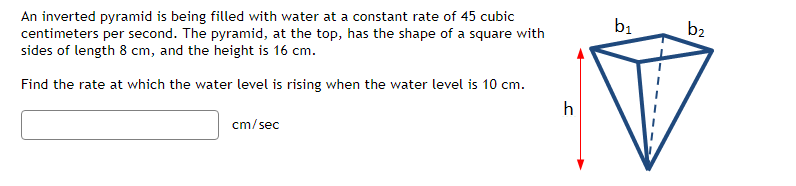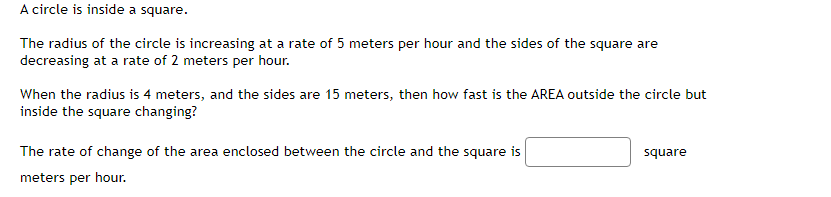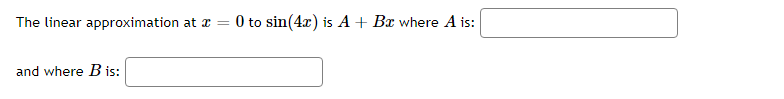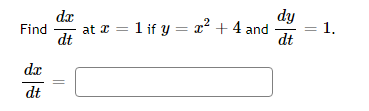
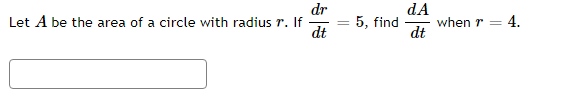
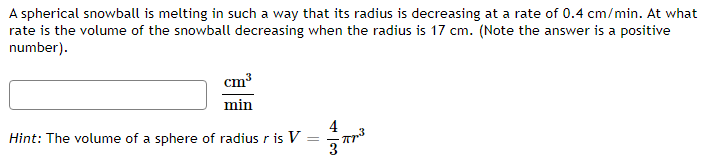




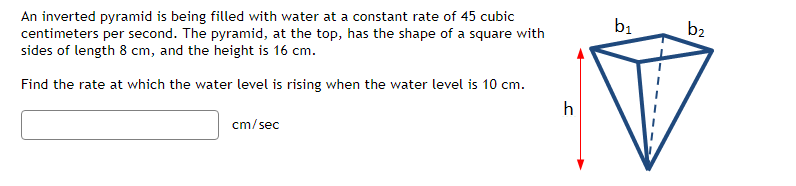
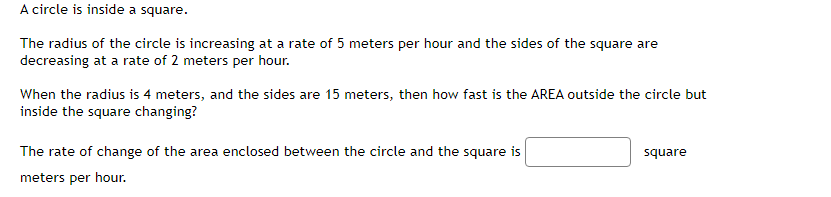



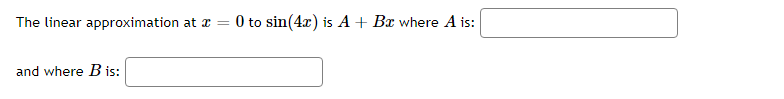





Calculus Questions (4.1 & 4.2)
1.
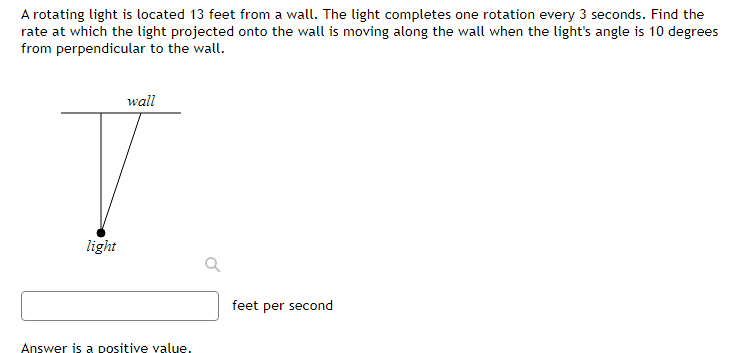
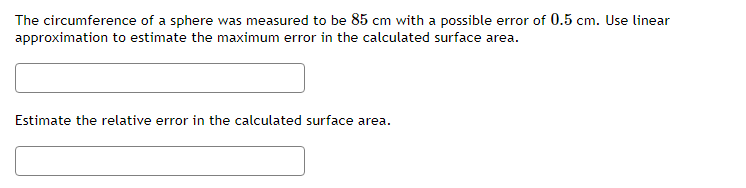
dy Find at = = 1ify= = +4 and = 1 dt dt dtdr dA Let A be the area of a circle with radius r. If = 5, find dt when r = 4. dtA spherical snowball is melting in such a way that its radius is decreasing at a rate of 0.4 cm/min. At what rate is the volume of the snowball decreasing when the radius is 17 cm. (Note the answer is a positive number). cm min Hint: The volume of a sphere of radius r is V=The altitude of a triangle is increasing at a rate of 1.5 centimeters}r minute while the area of the triangle is increasing at a rate of 2 square centimeters;Ir minute. At what rate is the base of the triangle changing when the altitude is 11 centimeters and the area is 33 square centimeters? Gravel is being dumped from a. conveyor belt at a rate of El] cubic feet per minute. It forms a pile in the shape of a right circular cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 21 feet high? Recall that the volume of a right circular cone with height h and radius of the base 1' is given by 1 V = szh ft m A rotating light is located '13 feet from a wall. The light completes one rotation everyr 3 seconds. Find the rate at which the light projected onto the wall is moving along the wall when the light's angle is 10 degrees from perpendicular to the wall. wolf Eight CL Answer is a positive value. At noon, ship it is 30 nautical miles clue west of ship B. Ship A is sailing west at 24 knots and ship B is sailing north at 25 knots. Howsr fast {in knots]: is the distance between the ships changing at 3 PM? (Note: 1 knot is a speed of 1 nautical mile per hour.) A street light is at the top of a 16 ft tall pole. A woman 6 ft tall walks away from the pole with a speed of 4 ft/sec along a straight path. How fast is the tip of her shadow moving when she is 30 ft from the base of the pole? ft secAn inverted pyramid is being filled with water at a constant rate of 45 cubic centimeters per second. The pyramid, at the top, has the shape of a square with sides of length 3 cm, and the height is 16 cm. Find the rate at which the water level is rising when the water level is 10' cm. Acircle is inside a square. The radius of the circle is increasing at a rate of 5 meters per hour and the sides of the square are decreasing at a rate of 2 meters per hour. When the radius is 4 meters, and the sides are 15 meters, then how fast is the AREA outside the circle but inside the square changing? The rate of change of the area enclosed between the circle and the square is :] square meters per hour. A police car is located Ell} feet to the side of a straight road. A red car is driving along the road in the direction of the police car and is 1311] feet up the road from the location of the police car. The police radar reads that the distance between the police car and the red car is decreasing at a rate of El} feet per second. How.r fast is the red car actuallyr traveling along the road? The actual speed {along the road] of the red car is feet per second Use linear approximation, i.e. the tangent line, to approximate \"15.3 as follows: Let ffz} = . Find the equation of the tangent line to x) at z = 15 Liz} = Using this, we find our approximation for 1:\"163 is NOTE: For this part, give your answer to at least 9 significant figures or use an expression to give the exact answer. 1 1 .5l]3 as follows: Let f[.') = E and find 1 the equation of the tangent line to f{z} at a "nice" point near H.503. Then use this to approximate U 5'13 Use linear approximation, i.e. the tangent line, to approximate The linear approximation at = 0 to sin(4x) is A + Ba where A is: and where B is:Use linear approximation, i.e. the tangent line, to approximate V27.4 as follows: Let f(x) = VT. The equation of the tangent line to f(@) at _ = 27 can be written in the form y = mr +b where m is: and where b is: Using this, we find our approximation for V27.4 isGiven the function below f(x) = V-50c + 175 Find the equation of the tangent line to the graph of the function at I = 1. Answer in max + b form. L(I) = Use the tangent line to approximate f(1.1). L(1.1) = Compute the actual value of f(1.1). What is the error between the function value and the linear approximation? Answer as a positive value only. |error | ( Approximate to at least 5 decimal places.)The circumference of a sphere was measured to be 35 cm with a possible error of ll cn1. Use linear approximation to estimate the maximum error in the calculated surface area. Estimate the relative error in the calculated surface area. Let y = tan{5:r: + 5). Find the differential y when 1' = 1 and dz = [LE :] Find the differential y when 1' = 1 and {is = ll :] Let y = 2.12. Find the change in 1;, y when .1: = 3 and 13 = 0.3 :] Find the differential y when 3: = 3 and {13: = \".3 :] Let y = 51/5. Find the change in 1;, y when a: = 2 and ns 2 {1.3 Find the differential y when a: = 2 and dz 2 DB