Can someone explain how to get the answers to this please

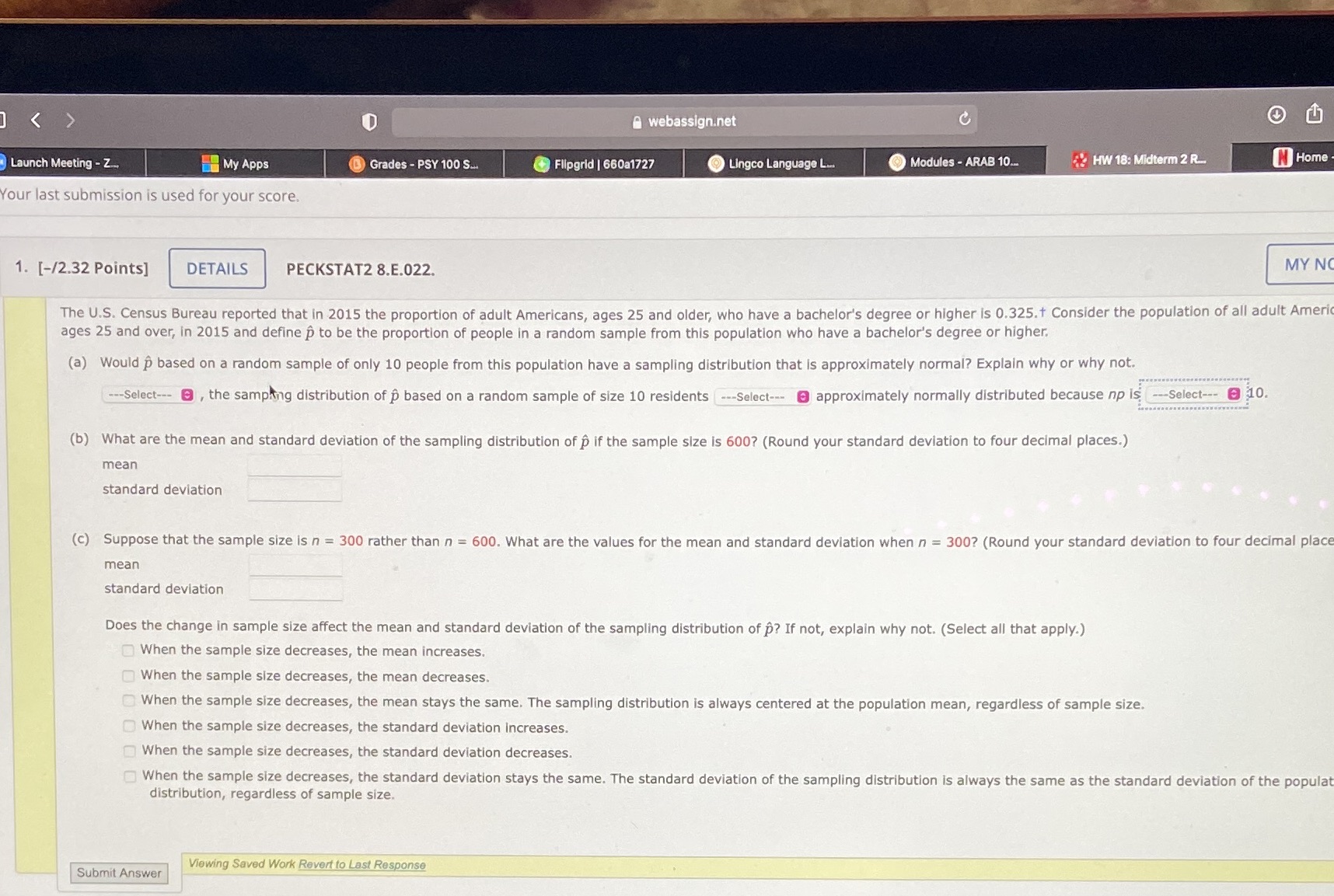
webassign.net O d Grades - PSY 100 S. Flipgrid | 660a1727 Lingco Language L. Modules - ARAB 10.. HW 18: Midterm 2 R_ N Home Launch Meeting - Z... My Apps our last submission is used for your score. 1. [-/2.32 Points] DETAILS PECKSTAT2 8.E.022. MY N The U.S. Census Bureau reported that in 2015 the proportion of adult Americans, ages 25 and older, who have a bachelor's degree or higher is 0.325. + Consider the population of all adult Ameri ages 25 and over, in 2015 and define p to be the proportion of people in a random sample from this population who have a bachelor's degree or higher. (a) Would p based on a random sample of only 10 people from this population have a sampling distribution that is approximately normal? Explain why or why not. ---Select--- @ , the sampling distribution of p based on a random sample of size 10 residents ---Select--- @ approximately normally distributed because np is --Select--- @ 10. (b) What are the mean and standard deviation of the sampling distribution of p if the sample size is 600? (Round your standard deviation to four decimal places.) mean standard deviation (c) Suppose that the sample size is n = 300 rather than n = 600. What are the values for the mean and standard deviation when n = 300? (Round your standard deviation to four decimal place mean standard deviation Does the change in sample size affect the mean and standard deviation of the sampling distribution of p? If not, explain why not. (Select all that apply.) When the sample size decreases, the mean increases. When the sample size decreases, the mean decreases. When the sample size decreases, the mean stays the same. The sampling distribution is always centered at the population mean, regardless of sample size. When the sample size decreases, the standard deviation increases. When the sample size decreases, the standard deviation decreases. When the sample size decreases, the standard deviation stays the same. The standard deviation of the sampling distribution is always the same as the standard deviation of the populat distribution, regardless of sample size. Submit Answer Viewing Saved Work Revert to Last Response