Can someone help me with part (b). I already got the solution for part (a) and I do not understand part (b). Thanks

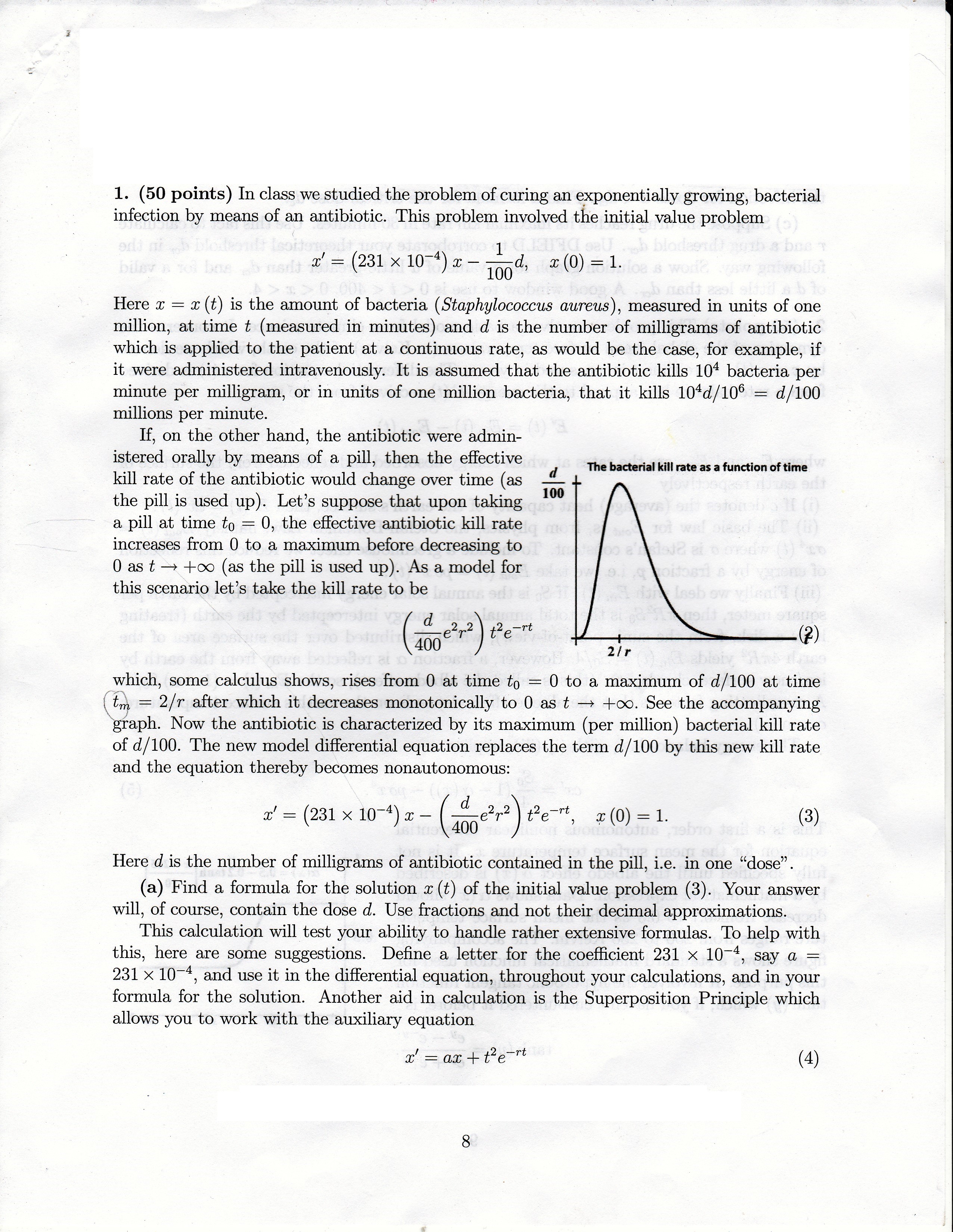
1. (50 points) In class we studied the problem of curing an exponentially growing, bacterial infection by means of an antibiotic. This problem involved the initial value problem {1}]: (231 x 10-4) cc at, a: (0) = 1. Here a: = x (t) is the amount of bacteria (Staphylococcus aureus), measured in units of one million, at time t (measured in' minutes) and d is the number of milligrams of antibiotic which is applied to the patient at a continuous rate, as would be the case, for example, if it were administered intravenously. It is assumed that the antibiotic kills 10'1 bacteria per minute per milligram, or in units of one million bacteria, that it kills 104d/106 = d/ 100 millions per minute. If, on the other hand, the antibiotic were admin- istered orally by means of a pill, then the effective a! m, ,immwa'ammam kill rate of the antibiotic would change over time (as the pill, is used up). Let's suppose that upon taking 100 a pill at time to = 0, the effective antibiotic kill rate increases from 0 to a maximum before decreasing to O as t > +00 (as the pill is used up). As amodel for this scenario let's take the kill rate to be d 2 2) 2 rt .e r t e , ) (400 2n (2 which, some calculus shows, rises from 0 at time to = 0 to a maximum of d/ 100 at time (:7 = 2/7' after which it decreases monotonically to 0 as t > +00. See the accOmpanying aph. Now the antibiotic is characterized by its maximum (per million) bacterial kill rate of d/ 100. The new model differential equation replaces the term (1/100 by this new kill rate and the equation thereby becomes nonautonomous: d I 4 22 2rt ac (231x10 )x (00er)te , $(0)-1. (3) Here d is the number of milligrams of antibiotic contained in the pill, i.e. in one \"dose\". (a) Find a formula for the solution a: (t) of the initial value problem (3). Your answer will, of course, contain the dose d. Use fractions and not their decimal approximations. This calculation will test your ability to handle rather extensive formulas. To help with this, here are some suggestions. Dene a letter for the coefcient 231 x 10-4, say a = 231 x 10-4, and use it in the differential equation, throughout your calculations, and in your formula for the solution. Another aid in calculation is the Superposition Principle which allows you to work with the auxiliary equation 33' = as: + t2?\" (4) since the q (t) term in the differential equation we Want to solve is a' multiple of this equation's q (t) term. ' (b) Use your solution formula from (a rove there is a critical dOSQUCh that the infection is_cured (i.e. x t = 0 at sour/I 1me t > 0) for doses (1 > dc, ut fails to cure the infection for doses d