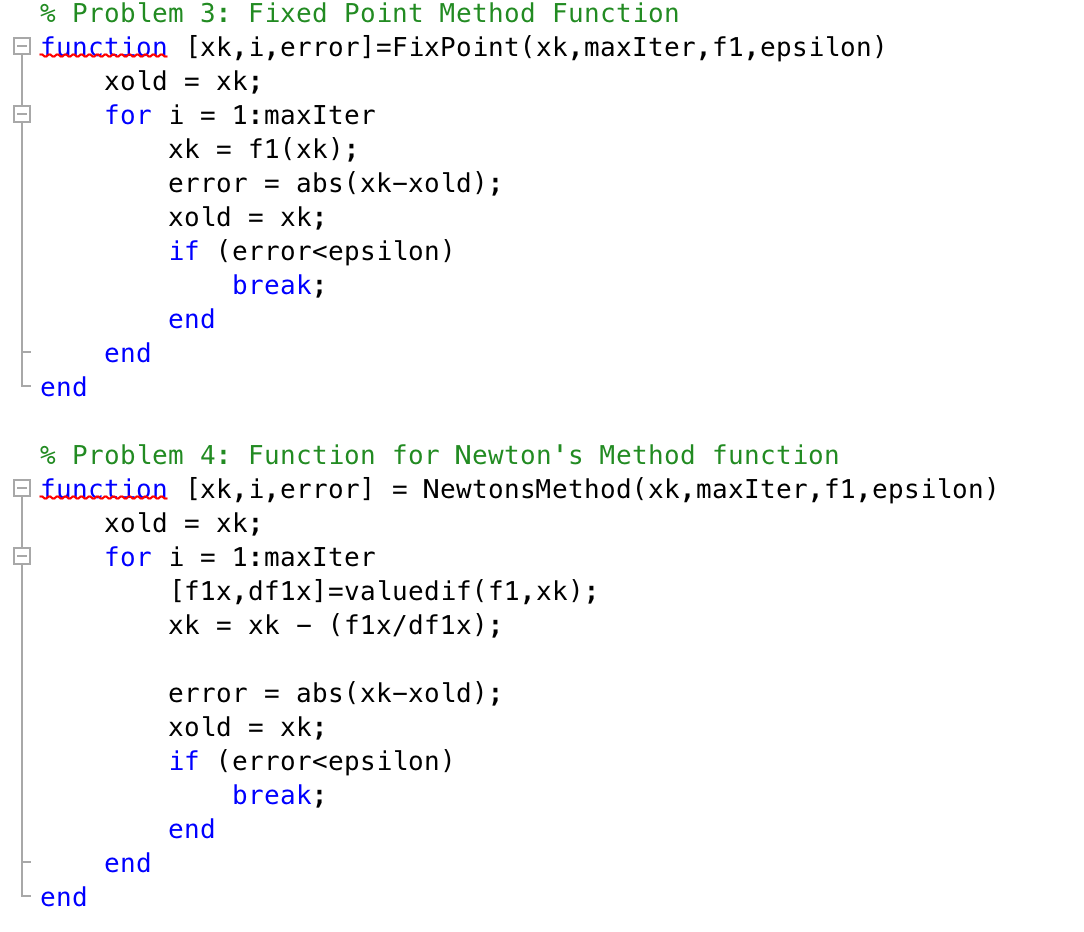
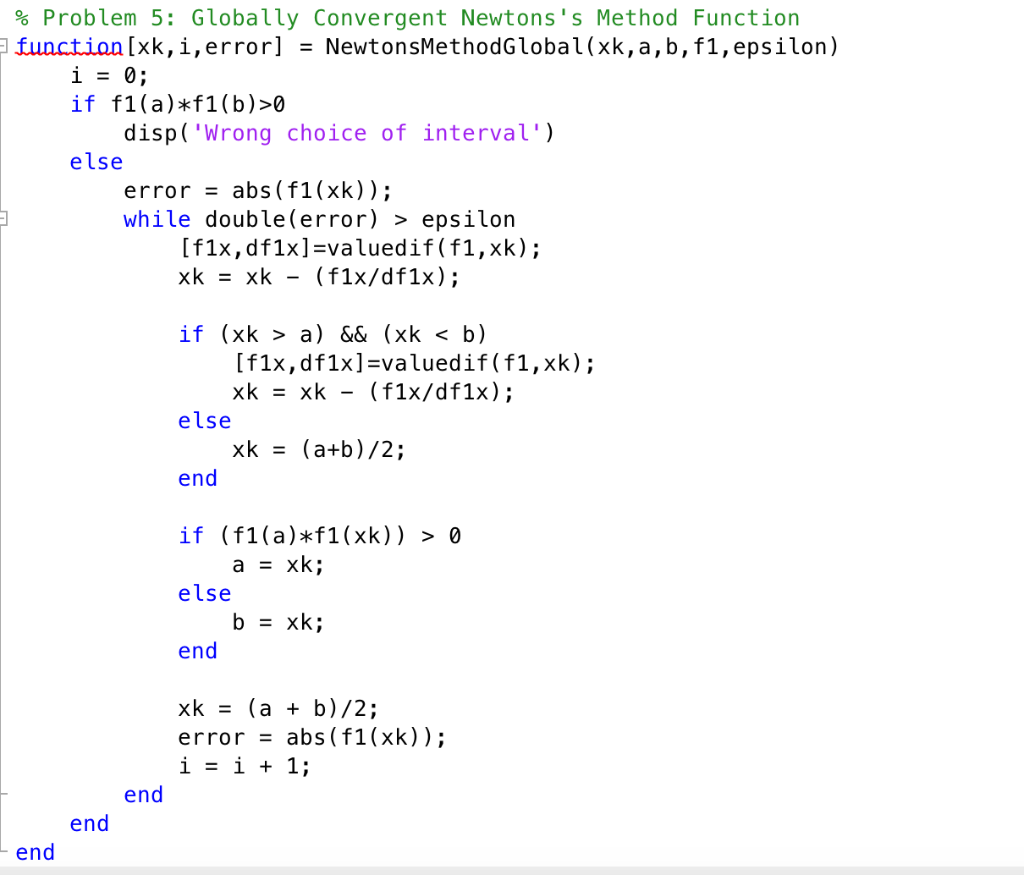
Can someone please do ALL question #6 by editing this part of the code I put below , and answering the question "which algorithm is both robust and fast"? I am not sure how to answer #6. I am using MATLAB. I can't get good graphs and not sure why. If possible can you edit the code I put above to get what #6. The code I want edited is this part:

clear; clc; a = -8; b = 8; maxIter = 1e6; %max iteration of the function epsilon = 10e-12; %tolerance value

f1 = @(x) exp(2*sin(x))-x; %function gx = @(x) asin(log(sqrt(x))); %alternative g(x) for problem 3 x0 = 2; %initial guess

% Problem 2: Calling the Interval Bisection Method Function [xk2,i2,error2] = Intbisections(f1,a,b,epsilon);

% Problem 3: Calling the Fixed Point Method Function [xk3,i3,error3] = FixPoint(x0,maxIter,gx,epsilon);

% Problem 4: Calling the Newton's Method function Problem 4 [xk4,i4,error4] = NewtonsMethod(x0,maxIter,f1,epsilon);

% Problem 5: Calling Globally Convergent Newtons's Method Function [xk5,i5,error5] = NewtonsMethodGlobal(x0,a,b,f1,epsilon);

%saving errors as vectors errorVector = [error2,error3,error4,error5];

%Graphing the error vector x_axis = [1,2,3,4]; %x-axis values semilogy(x_axis,errorVector,'-mo'); %graph of error vector in logarithmic y-axis grid on %logarithmic grid (y-axis only)

% Problem 1: Function for calling the value and the derivative of the function E function [xvalue,difx] = valuedif(f,xv) f(xv); xvalue = syms x if nargout > 1 g(x) difx = diff(f(x)); double(g(xv)); %3D end end % Problem 2: Interval Bisection Method Function function [xk,i,error] = Intbisections (f, a, b,epsilon) i = 1; if f(a)*f(b)>0 disp('Wrong choice of interval') else (a + b)/2; abs (f (xk)); while error > epsilon if f(a)*f(xk)>0 a = xk; xk = error = else b = xk; %3D end (a + b)/2; error = abs (f(xk)); i = i + 1; xk %| %| end end end % Problem 3: Fixed Point Method Function E function [xk,i,error]=FixPoint(xk,maxIter, f1,epsilon) xk; 1: maxIter xk = f1(xk); error = abs (xk-xold); xk; if (error0 disp('Wrong choice of interval') else error = abs(f1(xk)); while double(error) > epsilon [f1x,df1x]=valuedif(f1,xk); (f1x/df1x); xk = xk - if (xk > a) && (xk 0 a = xk; else b = xk; end xk = (a + b)/2; error = abs(f1(xk)); i = i + 1; end end Lend 6. Adjust the above functions such that for each of the four methods, you save the errors lex| for all the iterates into a vector. Draw the four error vectors for the four algorithms, respectively, in the same graph. Generate such graphs corresponding to different initial guesses used in the Newton's method, e.g., xo = -6, -4, 2, 0, 2, 4, 6, as done in Question 3, respectively. From those graphs, what can you say about the performances of the three algorithms? Which algorithm is both robust and fast? % Problem 1: Function for calling the value and the derivative of the function E function [xvalue,difx] = valuedif(f,xv) f(xv); xvalue = syms x if nargout > 1 g(x) difx = diff(f(x)); double(g(xv)); %3D end end % Problem 2: Interval Bisection Method Function function [xk,i,error] = Intbisections (f, a, b,epsilon) i = 1; if f(a)*f(b)>0 disp('Wrong choice of interval') else (a + b)/2; abs (f (xk)); while error > epsilon if f(a)*f(xk)>0 a = xk; xk = error = else b = xk; %3D end (a + b)/2; error = abs (f(xk)); i = i + 1; xk %| %| end end end % Problem 3: Fixed Point Method Function E function [xk,i,error]=FixPoint(xk,maxIter, f1,epsilon) xk; 1: maxIter xk = f1(xk); error = abs (xk-xold); xk; if (error0 disp('Wrong choice of interval') else error = abs(f1(xk)); while double(error) > epsilon [f1x,df1x]=valuedif(f1,xk); (f1x/df1x); xk = xk - if (xk > a) && (xk 0 a = xk; else b = xk; end xk = (a + b)/2; error = abs(f1(xk)); i = i + 1; end end Lend 6. Adjust the above functions such that for each of the four methods, you save the errors lex| for all the iterates into a vector. Draw the four error vectors for the four algorithms, respectively, in the same graph. Generate such graphs corresponding to different initial guesses used in the Newton's method, e.g., xo = -6, -4, 2, 0, 2, 4, 6, as done in Question 3, respectively. From those graphs, what can you say about the performances of the three algorithms? Which algorithm is both robust and fast