can u please do it i also send some formulas thanks

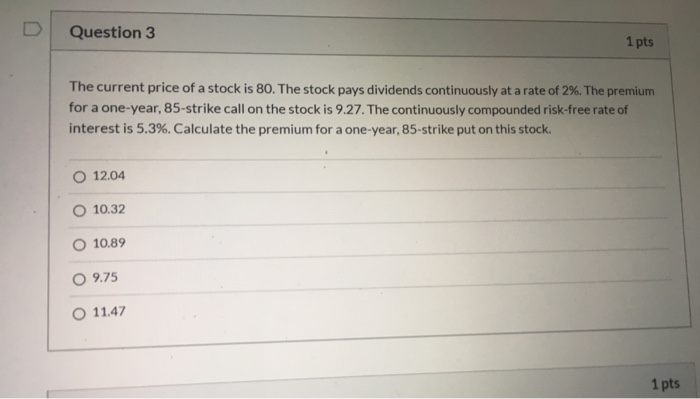
Question 3 1 pts The current price of a stock is 80. The stock pays dividends continuously at a rate of 2%. The premium for a one-year, 85-strike call on the stock is 9.27. The continuously compounded risk-free rate of interest is 5.3%. Calculate the premium for a one-year, 85-strike put on this stock. O 12.04 10.32 O 10.89 9.75 11.47 1 pts The process of calculating the correct premium for a put or call option is complicated, and is a task that we are not yet ready to fully undertake. However, by comparing the present values of cash flows generated by certain types of derivatives, one can determine a relationship between European put and European call premiums. This relationship is called put-call parity. Three versions of this relationship are stated below. General Put-Call Parity: Call K.T) - Put K.T) = PV (Far) - PV(K) Call K.T) - Put K.T) = F - PV(K) Put-Call Parity for Non-Dividend Stock: Call K.T) - PutKT) = S. - PV(K) Note that the put-call parity relationship only holds for European options. Derivation of Put-Call Parity Consider two derivative portfolios: Portfolio A contains one long call and one short put on an asset. Both options have a strike price of K, and both expire at time T. Convince yourself that regardless of the spot price of the asset at expiration, the owner of this portfolio will end up purchasing the asset for K at time T. Portfolio B consists only of a prepaid long forward contract expiring at time T. The underlying asset for the forward is the same as for the options in Portfolio A. Both portfolios will result in the owner of the portfolio receiving the asset at time T. In order to prevent arbitrage, the costs associated with the two portfolios should have the same present value. At time 0, the owner of Portfolio A will pay Call K.T) and will receive Put K. 7). The owner of Portfolio A will also pay K for the asset at time T. Thus, the present value of the total cost to the owner of Portfolio A is Call K, T) - Put K. 7) + PV(X). The only cash flow for the owner of Portfolio B is a payment of For at time 0. Setting the present values equal gives us Call(K.T) - Put K.T). PV(K) = F , which can be rewritten as Call K.7) - Put K.7) = F -PVK)