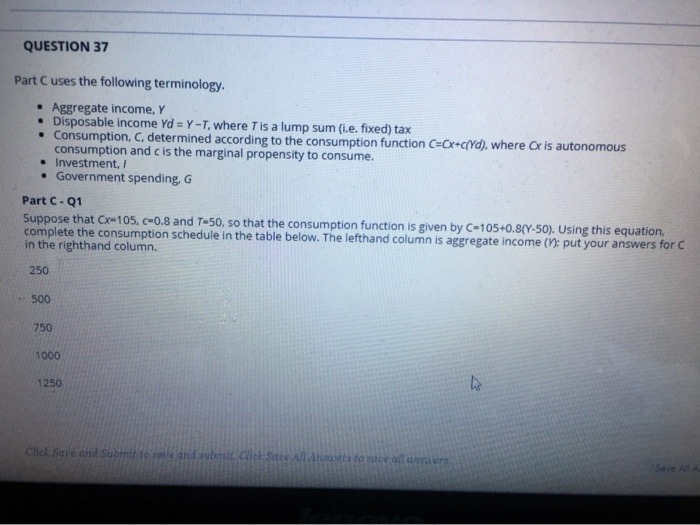
Can you help here.

Part 2 Consider the endogenous growth model in which time can be used for work (it) or human capital accumulation (1 15). Output is produced according to Y = zuH, where z is total factor productivity and H is the current stock of human capital. The future human capital stock is given by H ' = M] u)H, where 5 represents eiciency in producing new human capital. The initial (current) human capital stock is H = 100. The economy is characterized by the following parameters: b = 6.1, 2 = 15, and u = 0.83. (a) Calculate future human capital (H '), and the growth rate of human capital. (b) Calculate current output (Y), future output (1\"), and the growth rate of output. How does it compare to the growth rate of human capital? (c) Suppose the government cuts technology funding for education, and as a result b declines to b = 6.0. Calculate the growth rate of output following this change. ((1) Are the growth rates you found in parts a and c the same or different? Explain intuitively why this policy change did or did not a'ect the economy's growth rate. (e) Explain how the decrease in b will affect (if at all) the current levels of human capital, output, and consumption: H, Y, and C. If there is no effect, explain why. (f) Explain how the decrease in b will affect (if at all) the future levels of human capital, output, and consumption: H', Y' , and C' . If there is no effect, explain why. (g) Explain how the decrease in b will affect the growth rates of human capital, output, and consumption. If there is no effect, explain why. (h) Draw a graph of logoutput, ln'), over time for this economy and illustrate how the decrease in b affects current and future output. Chapter 5: Practice The following information applies to questions 1 - 8. Suppose we have the following information for the simple (fixed r, fixed P, fixed W) Keynesian model. C = 400 + 0.75 YD I = 340 G = 210 = 400 + 0.75 (Y - T) T = 200, where C is the consumption function, Yp is disposable income, I is investment, G is government spending, and T is taxes.2. Optimal Consumption Growth Consider a consumer who receives income Y at the beginning of period * = 0, which he or she divides up into an amount co to be consumed and an amount s to be saved, subject to Y 20+8. Suppose that the consumer receives no additional income in period f = 1, so that all of his or her consumption during that period has to be purchased with the savings and the interest earned on savings from period t = 0. Letting r denote the interest rate, this means that (1 + r)s 2 91. As in class, we can combine these two single-period constraints to obtain the consumer's "lifetime" budget constraint CI Yzotitr Suppose, further, that the consumer's preferences over consumption during the two periods are described by the utility function In(co) + B In(c). where B, satisfying 0