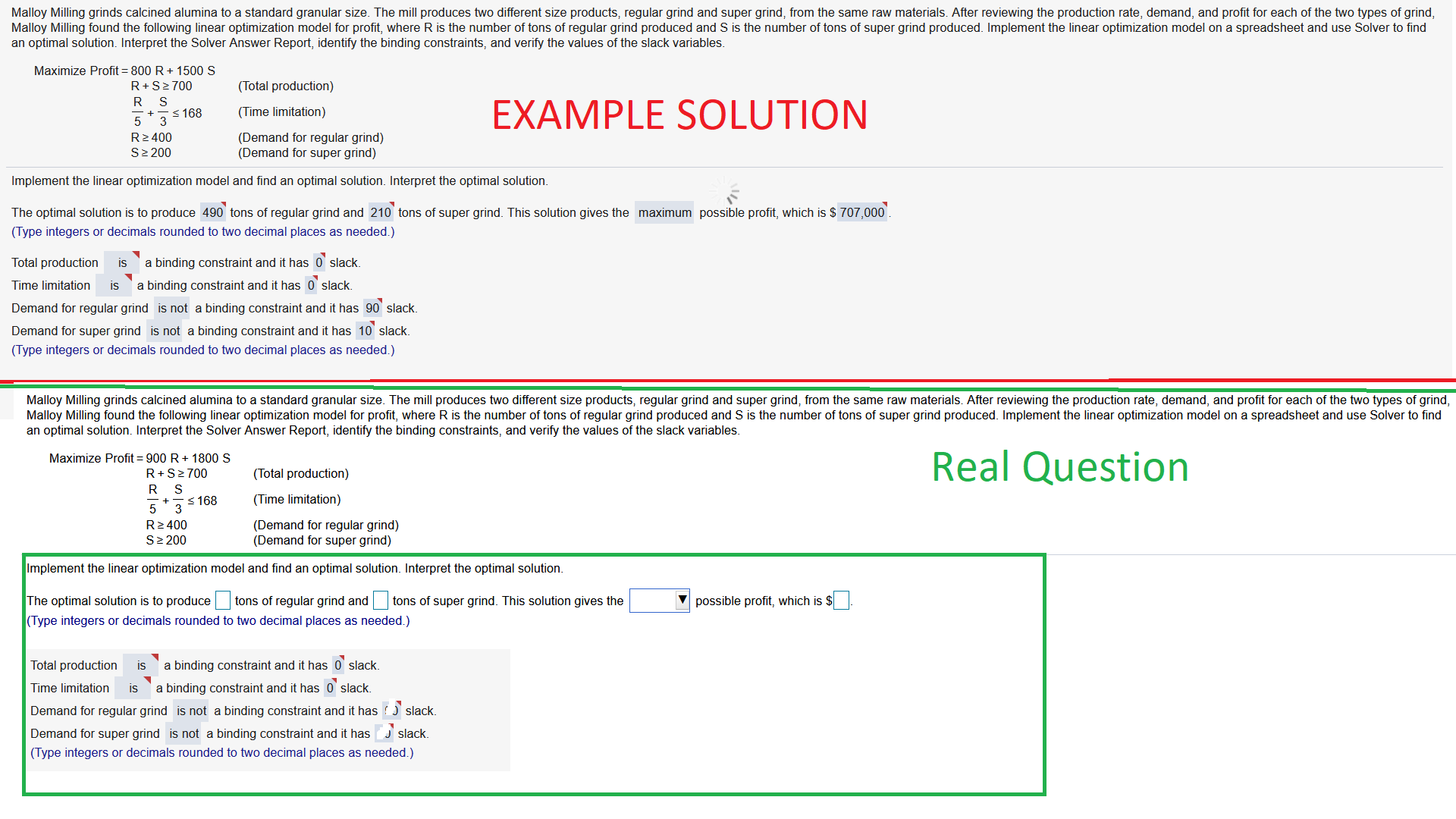
Can you help me find the solution using the SOLVER feature in Microsoft 365 excel? I have attached an example that is in red.... but my real question is located below it in GREEN. Thank you !
Malloy Milling grinds calcined alumina to a standard granular size. The mill produces two different size products, regular grind and super grind, from the same raw materials. After reviewing the production rate, demand, and profit for each of the two types of grind, Malloy Milling found the following linear optimization model for profit, where R is the number of tons of regular grind produced and S is the number of tons of super grind produced. Implement the linear optimization model on a spreadsheet and use Solver to find an optimal solution. Interpret the Solver Answer Report, identify the binding constraints, and verify the values of the slack variables. Maximize Profit = 800 R + 1500 S R + S 2 700 (Total production) RS + 3 $ 168 (Time limitation) EXAMPLE SOLUTION R 2 400 (Demand for regular grind) S 2 200 Demand for super grind) Implement the linear optimization model and find an optimal solution. Interpret the optimal solution. The optimal solution is to produce 490 tons of regular grind and 210 tons of super grind. This solution gives the maximum possible profit, which is $ 707,000. (Type integers or decimals rounded to two decimal places as needed.) Total production is a binding constraint and it has 0 slack. Time limitation is a binding constraint and it has 0 slack. Demand for regular grind is not a binding constraint and it has 90 slack. Demand for super grind is not a binding constraint and it has 10 slack. (Type integers or decimals rounded to two decimal places as needed.) Malloy Milling grinds calcined alumina to a standard granular size. The mill produces two different size products, regular grind and super grind, from the same raw materials. After reviewing the production rate, demand, and profit for each of the two types of grind, Malloy Milling found the following linear optimization model for profit, where R is the number of tons of regular grind produced and S is the number of tons of super grind produced. Implement the linear optimization model on a spreadsheet and use Solver to find an optimal solution. Interpret the Solver Answer Report, identify the binding constraints, and verify the values of the slack variables. Maximize Profit = 900 R + 1800 S R + S > 700 (Total production) Real Question R S 3 $ 168 (Time limitation) R 2 400 (Demand for regular grind) S 2 200 Demand for super grind) Implement the linear optimization model and find an optimal solution. Interpret the optimal solution. The optimal solution is to produce tons of regular grind and |tons of super grind. This solution gives the possible profit, which is $ Type integers or decimals rounded to two decimal places as needed.) Total production is a binding constraint and it has 0 slack. Time limitation is a binding constraint and it has 0 slack. Demand for regular grind is not a binding constraint and it has ? ) slack. Demand for super grind is not a binding constraint and it has J slack. (Type integers or decimals rounded to two decimal places as needed.)