Can you please derive this equation in an understandable way with the same final answer as the pictures

Thank you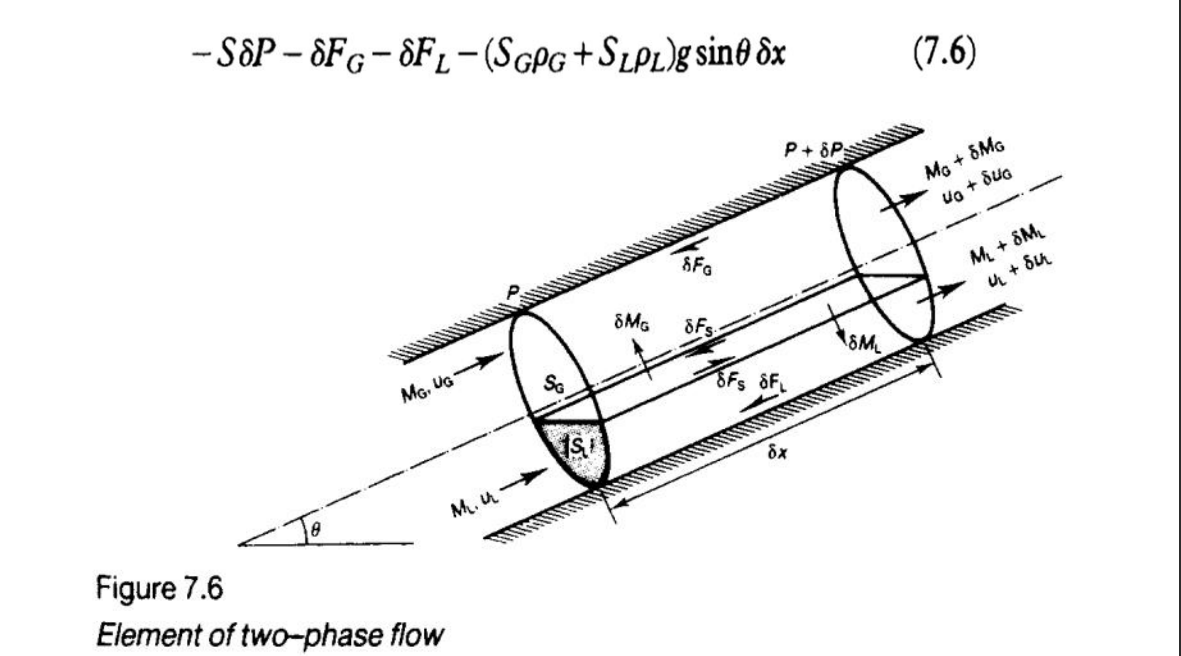

SPFGFL(SGG+SLL)gsinx Figure 7.6 Element of two-phase flow The terms represent the contributions from the total pressure gradient, the frictional drag of the pipe wall and the hydrostatic head of the two-phase mixture. The rate of change of momentum is (MG+MG)(uG+uG)+(ML+ML)(uL+uL)MGuGMLuL where the first two terms are the momentum flow rate of the fluid leaving the element and the third and fourth terms are the momentum flow rates into the element. For steady flow the net force acting on the fluid in the element is equal to the change of momentum flow rate: SPFGFL(SGG+SLL)gsinx=(MGuG+MLuL) where second order terms have been neglected. Consequently, Afder dividing all the terms by dx SdxdPdxdF(SGG+SLL)gsin=dxd(MGuG+MLuL) The terms represent the contributions from the total pressure gradient, the frictional drag of the pipe wall and the hydrostatic head of the two-phase mixture. The rate of change of momentum is (MG+MG)(uG+uG)+(ML+ML)(uL+uL)MGuGMLuL where the first two terms are the momentum flow rate of the fluid leaving the element and the third and fourth terms are the momentum flow rates into the element. For steady flow the net force acting on the fluid in the element is equal to the change of momentum flow rate: SPFGFL(SGG+SLL)gsinx=(MGuG+MLuL) where second order terms have been neglected. Consequently, Afder dividing all the terms by dx SdxdPdxdF(SGG+SLL)gsin=dxd(MGuG+MLuL) SdxdPdxdF(SGG+SLL)gsin=dxd(MGuG+MLuL) or dxdP=S1dxdFS1dxd(MGuG+MLuL)(SSGG+SSLL)gsin Equation 7.10 shows that the total pressure gradient comprises three components that are due to fluid friction, the rate of change of momentum and the static head. The momentum term is usually called the accelerative component. Thus dxdP=(dxdP)f+(dxdP)a+(dxdP)sh In principle, this is the same as for single-phase flow. For example in steady, fully developed, isothermal flow of an incompressible fluid in a straight pipe of constant cross section, friction has to be overcome as does the static head unless the pipe is horizontal, however there is no change of momentum and consequently the accelerative term is zero. In the case of compressible flow, the gas expands as it flows from high pressure to low pressure and, by continuity, it must accelerate. In Chapter 6 this was noted as an increase in the kinetic energy. In gas-liquid flow with no change of phase, for example air and water, the gas phase expands and acceleration occurs as in single-phase flow. Where the two-phase flow may be dramatically different from single-phase flow is when boiling or condensation occurs. For example, in a boiling two-phase flow the relatively dense liquid is changed into a vapour having a much lower density (higher specific volume) and a substantial accelerative pressure gradient may be required