
CAN YOU PLEASE HELP ME ANSWER THE FOLLOWING MATH PROBLEMS, THANK YOU!
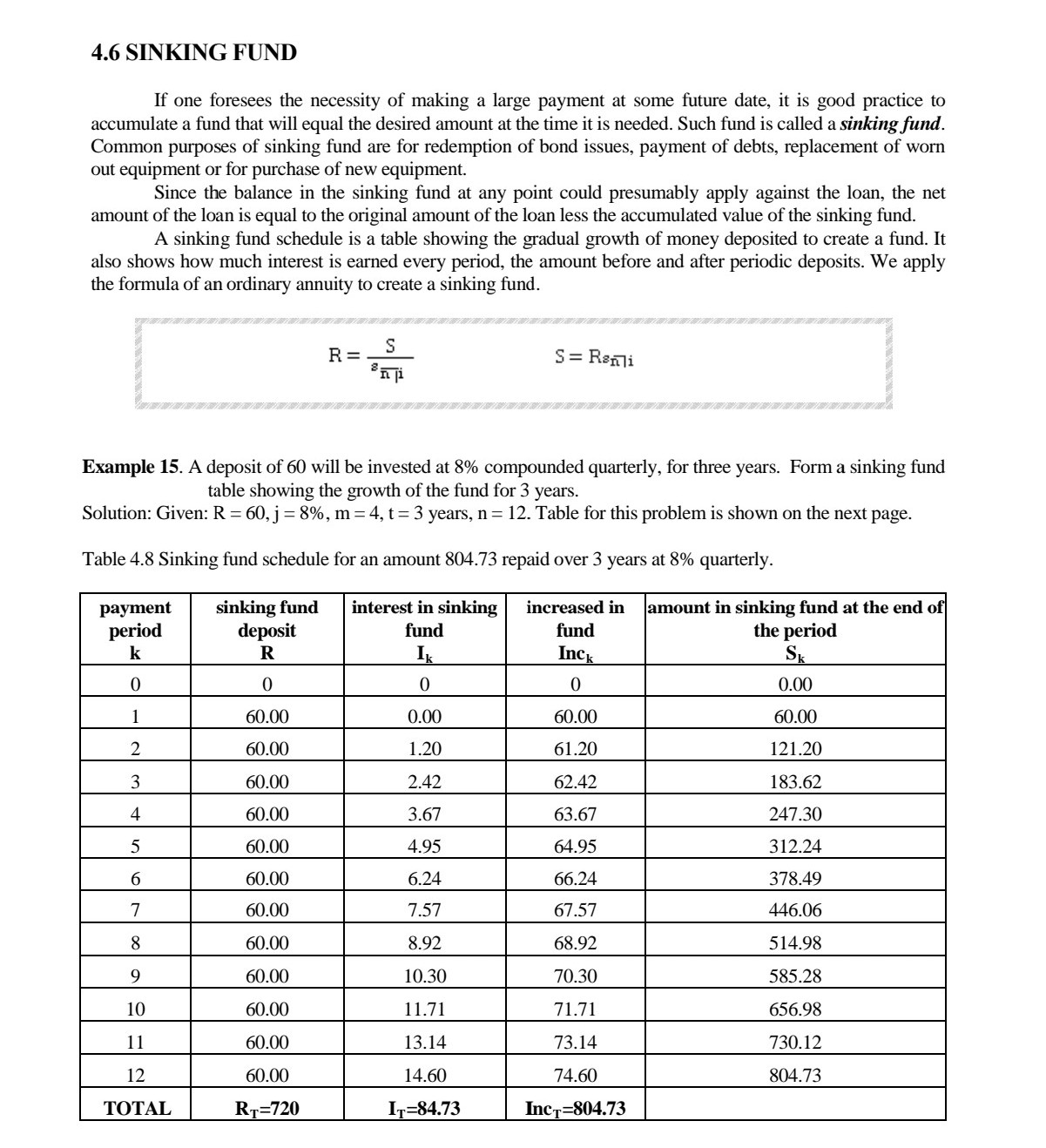
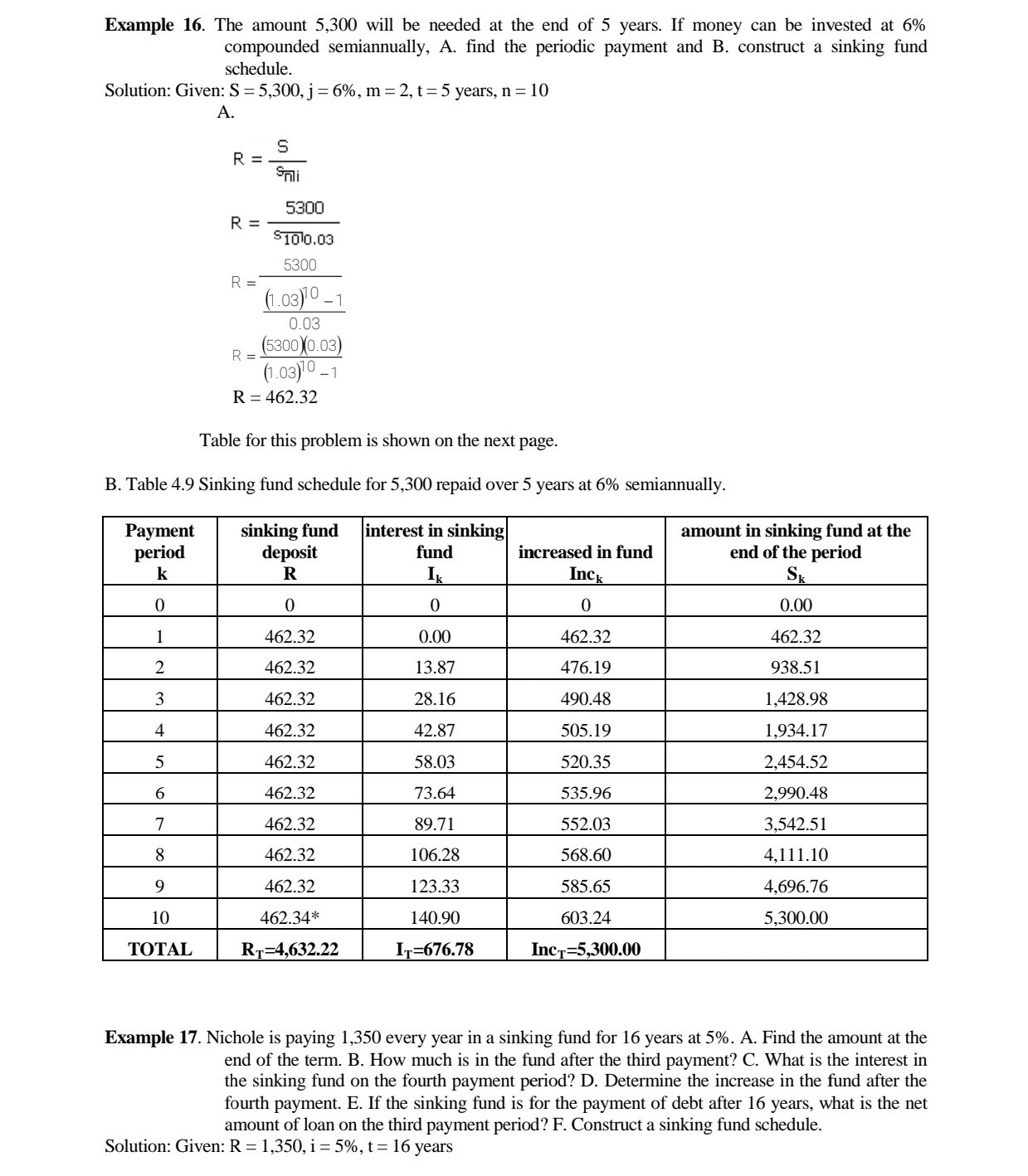
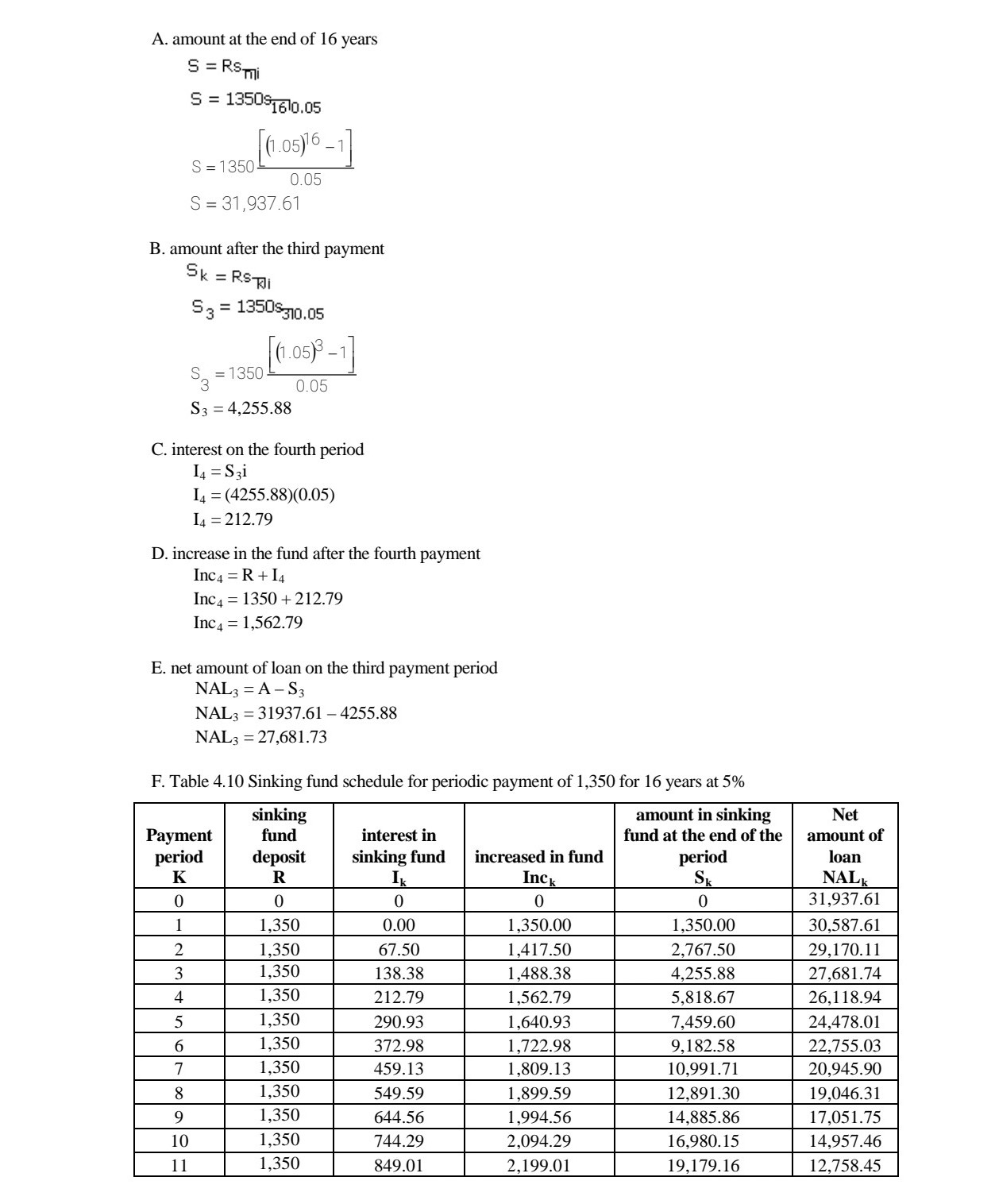
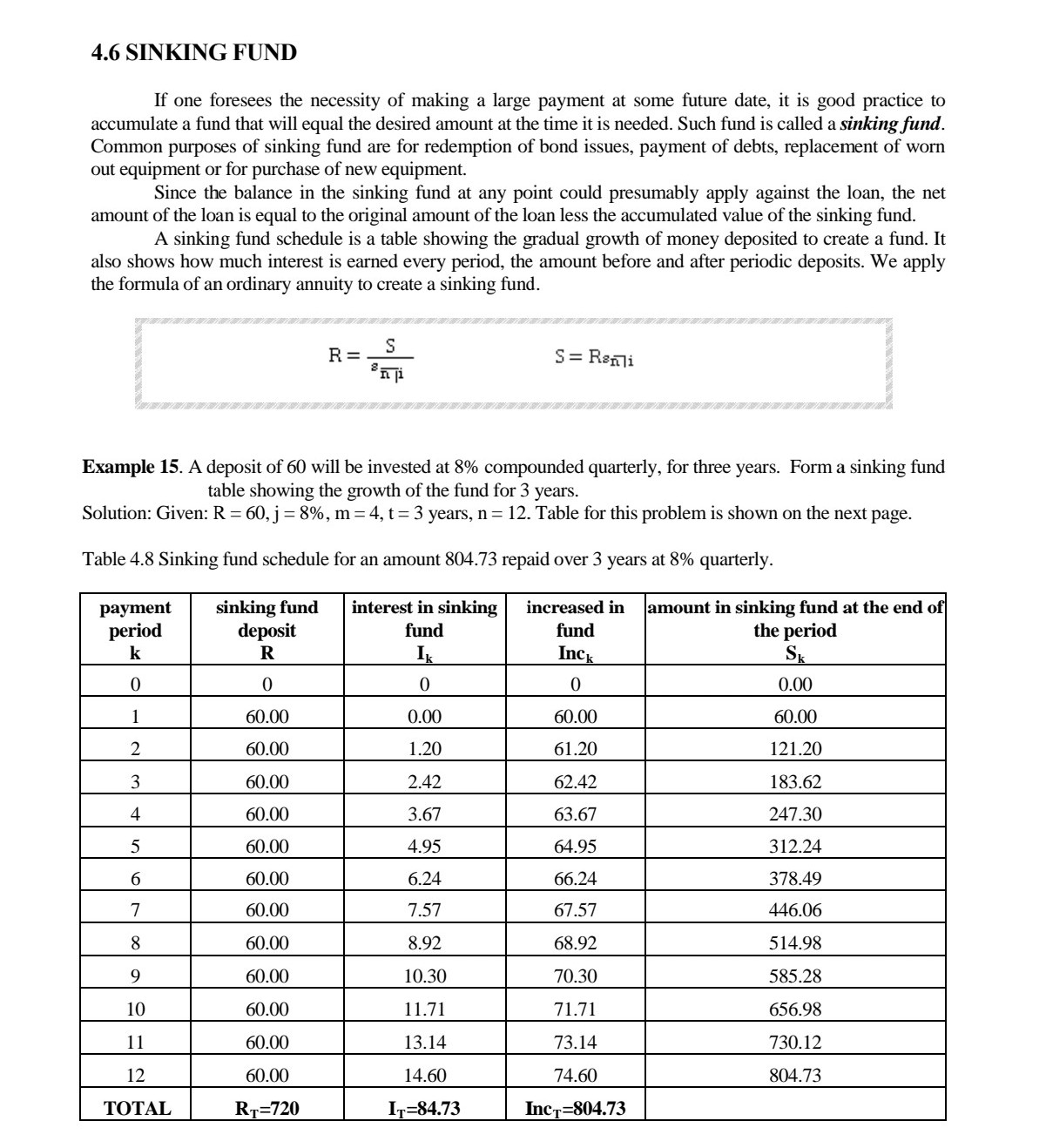
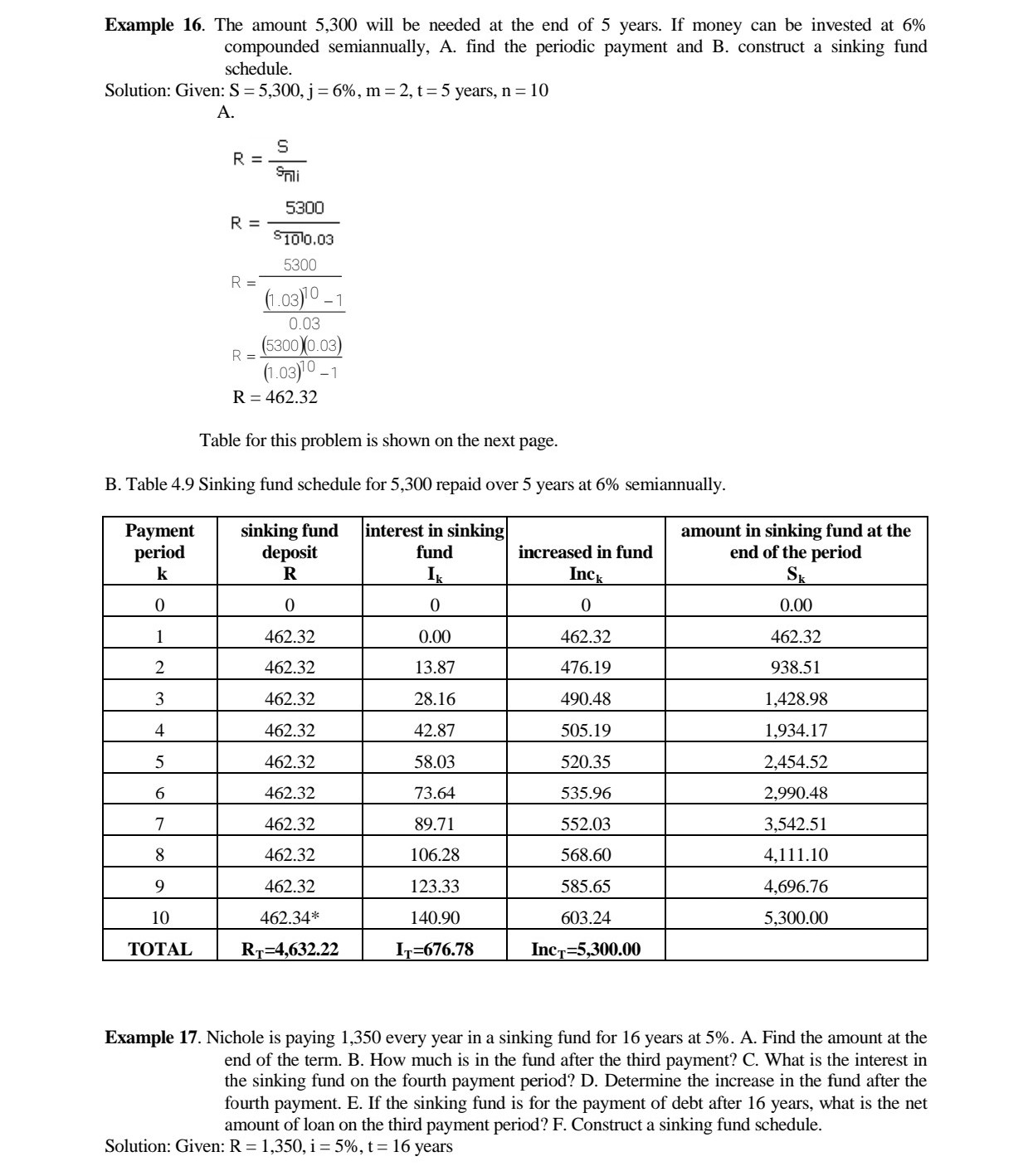
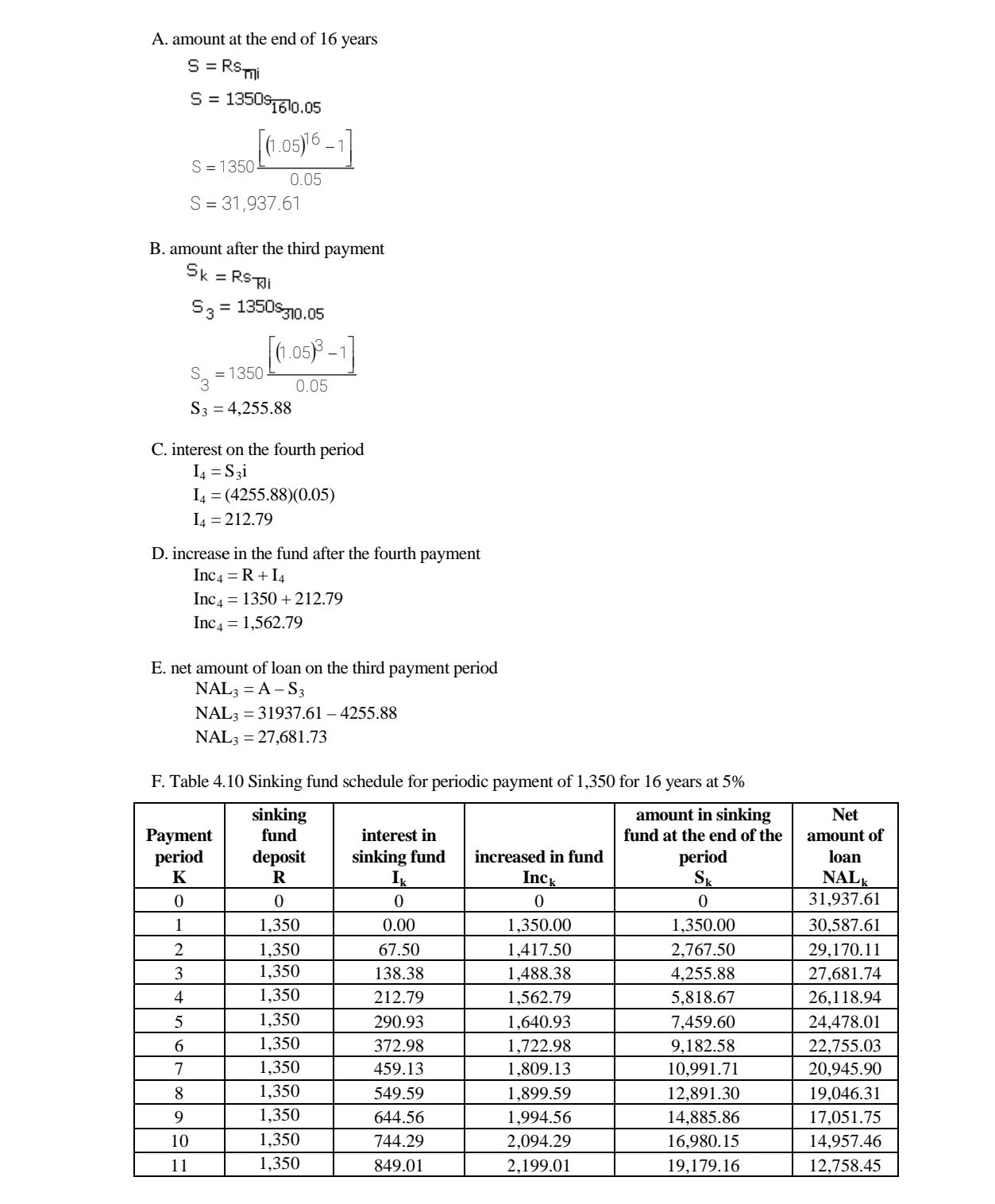
CHAPTER 4 EXERCISES 01. 02. 03. E. A debt is being discharged, interest at 6% payable semiannually, by payments of 1,000 at the end of each 6 months. At the beginning of the third year, the outstanding principal is 22,050.75. Make up the amortization schedule for the next year. How much principal is paid at the end of that year? In the purchase of a color television set, a buyer pays 2,000 cash. He will discharge the balance, by payments of 200 at the end of each month for a year. Assume that j : 6%. Find the cash value of the television set B) How much of the fourth monthly payment is interest and how much is repayment of the principal of the debt? A bank has granted a 2,000 home impnovement loan to a man, who agrees to pay 80 at the end of each month as long as necessary to pay all principal and interest at the rate 15% payable monthly. A) What is the remaining liability just after his fourth payment? B) How much principal does he repay on the fth payment date? C) Find his nal payment and when it is due. A young man decides that he must have 8,000 at the end of three years in order to make possible two years of college education. If he can invest at 5% compounded monthly, how much must he place in his fund at the end of each month? A loan of 80,000 is made with interest payable semiannually at the rate 3'96 compounded semiannually. Find the semiannual expense of the debt to the debtor, A. if he discharges all liability as to principal and interest by paying his creditor equal sums at the end of each 6 months for 7 years; B. If he pays interest as due and accumulates a sinking fund to pay the principal at the end of 7 years, with the fund invested at 4.5% compounded semiannually. 4.6 SIN KING FUND If one foresees the necessity of making a large payment at some future date, it is good practice to accumulate a fund that will equal the desired amount at the time it is needed. Such fund is called a sinkingfund. Common purposes of sinking fund are for redemption of bond issues, payment of debts, replacement of worn out equipment or for purchase of new equipment. Since the balance in the sinking flmd at any point could presumably apply against the loan, the net amount of the loan is equal to the original amount of the loan less the accumulated value of the sinking fund. A sinking fund schedule is a table showing the gradual growth of money deposited to create a fund. It also shows how much interest is earned every period, the amount before and after periodic deposits. We apply the formula of an ordinary annuity to create a sinking fund. S = Raf\" Example 15. A deposit of 60 will be invested at 8% compounded quarterly, for three years. Form a sinking fund table showing the growth of the fund for 3 years. Solution: Given: R : 60, j = 8%, m : 4, t: 3 years, n : 12- Table for this problem is shown on the next page. Table 4.8 Sinking fund schedule for an amount 804.73 repaid over 3 years at 8% quarterly. payment Sinking fund interest in Sinking increased in amount in sinking fund at the end 0 ' period deposit fund ' k R Ik 1|le Sk \"nu-n\" m- -_ m n n \"_ __ Example 16. The amount 5,300 will be needed at the end of 5 years. If money can be invested at 6% compounded semiannually, A. find the periodic payment and B. construct a sinking fund schedule. Solution: Given: S = 5,300, j = 6%, m = 2, t= 5 years, n = 10 A. S R = Soli 5300 = $1010.03 5300 R = (1.03)10 -1 0.03 R = (5300 )0.03) (1.03)10 -1 R = 462.32 Table for this problem is shown on the next page. B. Table 4.9 Sinking fund schedule for 5,300 repaid over 5 years at 6% semiannually. Payment sinking fund interest in sinking amount in sinking fund at the period deposit fund increased in fund end of the period k R Ik Inck SK 0 0 0 0.00 1 462.32 0.00 462.32 462.32 2 462.32 13.87 476.19 938.51 3 462.32 28.16 490.48 1,428.98 4 462.32 42.87 505.19 1,934.17 462.32 58.03 520.35 2,454.52 6 462.32 73.64 535.96 2,990.48 7 462.32 39.71 552.03 3,542.51 8 462.32 106.28 568.60 4,111.10 9 462.32 123.33 585.65 4,696.76 10 462.34* 140.90 603.24 5,300.00 TOTAL RT=4,632.22 IT=676.78 IncT=5,300.00 Example 17. Nichole is paying 1,350 every year in a sinking fund for 16 years at 5%. A. Find the amount at the end of the term. B. How much is in the fund after the third payment? C. What is the interest in the sinking fund on the fourth payment period? D. Determine the increase in the fund after the fourth payment. E. If the sinking fund is for the payment of debt after 16 years, what is the net amount of loan on the third payment period? F. Construct a sinking fund schedule. Solution: Given: R = 1,350, i = 5%, t = 16 yearsA. amount at the end of 16 years S = RSmi S = 1350$1610.05 (1.05)16 -1 S = 1350 0.05 S = 31,937.61 B. amount after the third payment SK = RSJI Sa = 1350$310.05 (1.05) 3 -1] S, = 1350. 0.05 S3 = 4,255.88 C. interest on the fourth period 14 = S31 14 = (4255.88)(0.05) 14 = 212.79 D. increase in the fund after the fourth payment Inc4 = R + 14 Inc4 = 1350 + 212.79 Inc4 = 1,562.79 E. net amount of loan on the third payment period NAL3 = A - S3 NAL3 = 31937.61 -4255.88 NAL3 = 27,681.73 F. Table 4.10 Sinking fund schedule for periodic payment of 1,350 for 16 years at 5% inking amount in sinking Net Payment fund interest in fund at the end of the amount of period deposit sinking fund increased in fund period loar K R Ik Inck Sk NAL 0 0 0 0 31,937.61 ,350 ).00 ,350.00 ,350.00 30,587.61 1,350 $7.50 1,417.50 2,767.50 29,170.11 1,350 138.38 1,488.38 1,255.88 27,681.74 1,350 212.79 ,562.79 5,818.67 26,118.94 1,350 290.93 1,640.93 7,459.60 24,478.01 5 6 0 Va UI A W N - 1,350 372.98 1,722.98 9,182.58 22,755.03 1,350 459.13 ,809.13 0,991.71 20,945.90 ,350 549.59 ,899.59 2,891.30 19,046.31 1,350 644.56 1,994.56 4,885.86 17,051.75 1,350 744.29 2,094.29 6,980.15 14,957.46 11 1,350 849.01 2,199.01 19,179.16 12,758.45SUMMARY OF FORMULAS 1. Amortization 2. Sinking fund A = Rami S = RS mi S A R = - R = Uni Smi 3. Outstanding Principal a. prospective method b. retrospective method OPK = Ron-k+lli OPK = A(1+1) *- K-1 - RSK-Ti 4. Principal and Interest included in any amortization payment IK = 1OPk PK = R -IK OPK = OPK-1 - Pk-1 5. Approximation of amortization rate a. Maximum Yield Method 21 im 2ril i'm =- or A ( n + 1 ) - 1 (n- 1) A( n + 1 ) - 1(n-1) b. Minimum Yield Method 21 2ml Im = - or A(n + 1 ) + 1 (n- 1 ) jm = A(n + 1 ) + 1 (n- 1 ) c. Constant Ratio Method 21 2ml lor =7 or Jer A ( n+ 1 ) A ( n+ 1 ) d. Direct Ratio Method 21 2ml | dr or Jar A ( n + 1 ) + = 1 (n-1 ) A ( n + 1 ) + - 1 ( n - 1 ) e. averaging formula nR - A j = n A +R X100xm 2