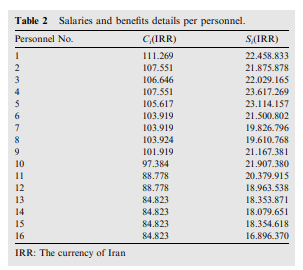
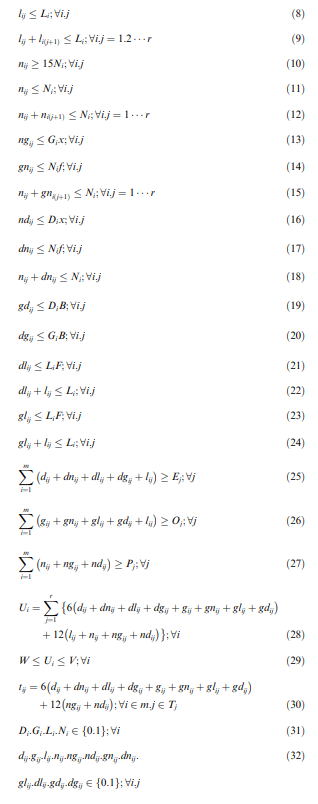
can you please write this problem on lingo

\begin{tabular}{lll} Table 2 & Salaries and benefits details per personnel. \\ \hline Personnel No. & Ci( IRR ) & Si( IRR ) \\ \hline 1 & 111.269 & 22.458 .833 \\ 2 & 107.551 & 21.875 .878 \\ 3 & 106.646 & 22.029 .165 \\ 4 & 107.551 & 23.617 .269 \\ 5 & 105.617 & 23.114 .157 \\ 6 & 103.919 & 21.500 .802 \\ 7 & 103.919 & 19.826 .796 \\ 8 & 103.924 & 19.610 .768 \\ 9 & 101.919 & 21.167 .381 \\ 10 & 97.384 & 21.907 .380 \\ 11 & 88.778 & 20.379 .915 \\ 12 & 88.778 & 18.963 .538 \\ 13 & 84.823 & 18.353 .871 \\ 14 & 84.823 & 18.079 .651 \\ 15 & 84.823 & 18.354 .618 \\ 16 & 84.823 & 16.896 .370 \\ \hline IRR: The currency of Iran & & \end{tabular} \begin{tabular}{llllll} \hline Table 1 & Model Parameters. & & & \\ \hline & & x & f & B & F \\ \hline 0.4 & 0.35 & 8 & 8 & 11 & 11 \\ \hline \end{tabular} Uitij0;ij The objective function (1) is regarding minimization of the total variable cost of payrolls, including base pay, benefits, overtime, and overnight payments. Constraint (2) ensures that each staff member is assigned exactly one shift. Constraint (3) ensures that staff with morning (D) shifts must work at least 26 days in a month for this shift to complete 180h of work, which is the minimum working time of each staff (W). Constraint (4) ensures that staff who selected for morning shifts work at morning shifts. Constraint (5) ensures that staff with evening (G) shifts must work at least 26 days in a month for this shift to complete 180h of work. Constraint (6) ensures that staff who selected for evening shifts work at evening shifts. Constraint (7) ensures that staff with morning and evening (L) shifts must work at least 15 days in a month for this shift to complete 180h of work. Constraint (8) ensures that staff who selected for morning and evening shifts work at this shift. Constraint (9) ensures that staff who worked at morning and evening shifts be off the next day to comply with the 12hours work 24-hours off rule. Constraint (10) ensures that staff with night (N) shifts must work at least 15 days in a month for this shift to complete 180h of work. Constraint (11) ensures that staff who selected for night shifts work at this shift. Constraint (12) ensures that staff who worked at night shifts be off the next day to comply with the 12 -hours work 24 -hours off rule. Constraint (13) states that staff with evening shifts may work up to night(s) as overtime. Constraint (14) states that staff with night shift may work up to f evening shift(s) as overtime. Constraint (15) ensures that the overtime evening shift for the night-shift staff must be the same shift before that night, to ensure staff satisfaction. Constraint (16) states that staff with morning shift may work up to night(s) as overtime. Constraint (17) states that staff with night shift may work up to f morning shift(s) as overtime. Constraint (18) ensures that the overtime morning shift for the night-shift staff must be the same shift after that night, to ensure staff satisfaction. Constraint (19) states that staff with morning shifts may work up to B evening shift(s) as overtime. Constraint (20) states that staff with evening shifts may work up to B morning shift(s) as overtime. Constraint (21) states that staff with morning and evening (L) shifts may work up to F days of morning shift(s) as overtime. Constraint (22) ensures that staff with morning and evening (L) shift just work at morning shift as overtime in the days which are not assigned to them as L shifts. Constraint (23) states that staff with morning and evening (L) shifts may work up to F days of evening shift(s) as overtime. Constraint (24) ensures that staff with morning and evening (L) shift just work at evening shift as overtime in the days which are not assigned to them as L shifts. Constraint (25) and (26) and (27) ensures supplying of the required number of staff in the morning, evening, and night, respectively. Equation (28) calculates the total working hours of each staff during a month. Constraint (29) ensures compliance with the minimum and maximum limits for working hours for each staff. Equation (30) calculates the total working hours of each staff during off days in a month. Binary variables are stated in equations (31) and (32), and continuous variables are stated in (33). lijLij;i.jlij+li(j+1)Li;i.j=1.2rnij15Ni;i.jnijNi;i.jnij+ni(j+1)Ni;i.j=1rngijGix;i.jgnijNijfi,jnij+gni(i+1)Ni;i.j=1rndijDix;i.jdnijNif;i,jnij+dnijNi;i,jgdijDiB;i,jdgijGiB;i.jdlijLiF;i.jdlij+lijLi;i.jglijLiF;i,jglij+lijLi;i,ji=1n(dij+dnij+dlij+dgij+lij)Ej;ji=1m(gij+gnij+glij+gdij+lij)Oij;ji=1nn(nij+ngij+ndij)Pj;jUi=j=1r{6(dij+dnij+dlij+dgij+gij+gnij+glij+gdij)+12(lij+nij+ngij+ndij)};iWUiV;itij=6(dij+dnij+dlij+dgij+gij+gnij+glij+gdij)+12(ngij+ndij);im.jTjDiGiLiNi{0.1};idijgijlijnijngijndijgnijdnijglijdli,jgdijdgij{0.1};ij : Percentage added to base salary for working on overtime or holiday : Percentage added to base salary for working on overnight Decision variables: Di : Binary variable determines if staff i works on the morning shift or not Gi : Binary variable determines if staff i works on the evening shift or not Li. Binary variable determines if staff i works on the morning and evening shift or not Ni. Binary variable determines if staff i works on the night shift or not dij : Binary variable determines if staff i works on the morning shift of day j or not gij : Binary variable determines if staff i works on the evening shift of day j or not Iij : Binary variable determines if staff i works on the morning and evening shift of day j or not nij. Binary variable determines if staff i works on the night shift of day j or not Ui : Total working hours of staff i tij : Total off-day working hours of staff i on day j ngij : Binary variable determines if G-type staff i works on the night shift of day j or not gnij : Binary variable determines if N-type staff i works on the evening shift of day j or not gliy : Binary variable determines if L-type staff i works on the evening shift of day j or not gdi: : Binary variable determines if D-type staff i works on the evening shift of day j or not ndij : Binary variable determines if D-type staff i works on the night shift of day j or not dnij : Binary variable determines if N-type staff i works on the morning shift of day j or not dliy : Binary variable determines if L-type staff i works on the morning shift of day j or not dgij : Binary variable determines if G-type staff i works on the morning shift of day j or not The proposed mathematical model with respect to the mentioned variables is as follows: MinZ=j=1m{(i=1mSi(Di+Gi+Li+Ni))+(Ci(UiW))+(Cij=1rtij)+Cij=1r(ndij+ngij+ni)} S.t: Di+Gi+Li+Ni=1;i dij26Di;i.j dijDi;i.j gij26Gi;i.j gijGi;i.j lij15Li;i.j