Can you translate this code to java

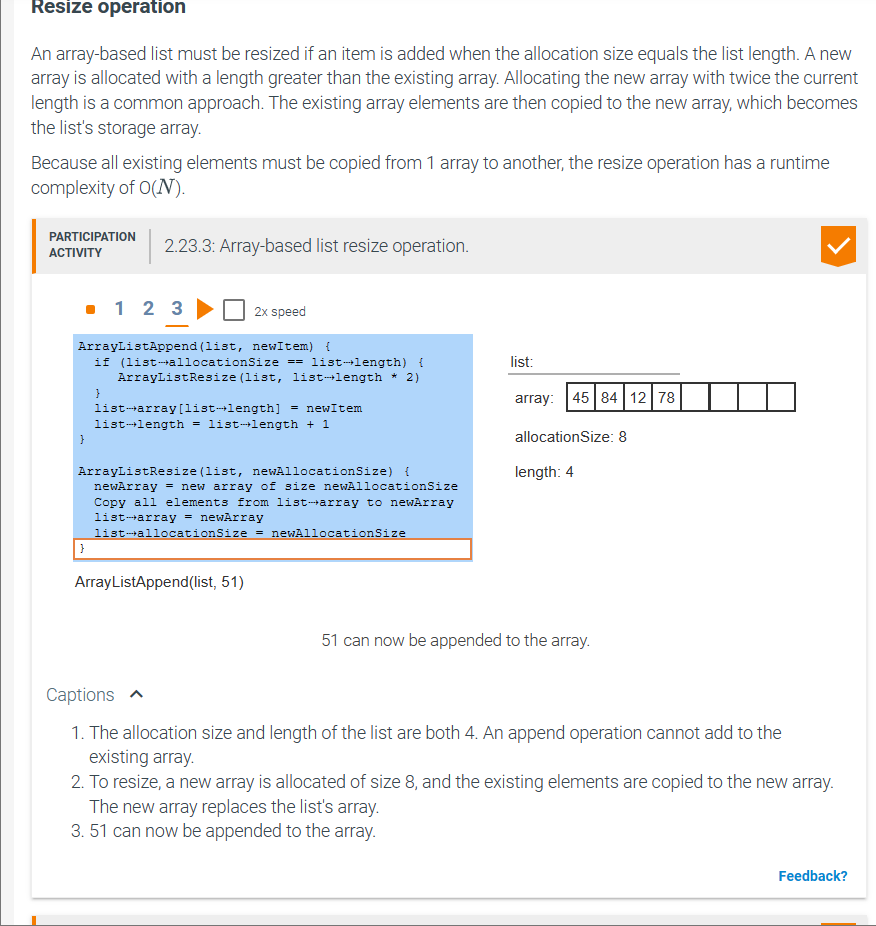
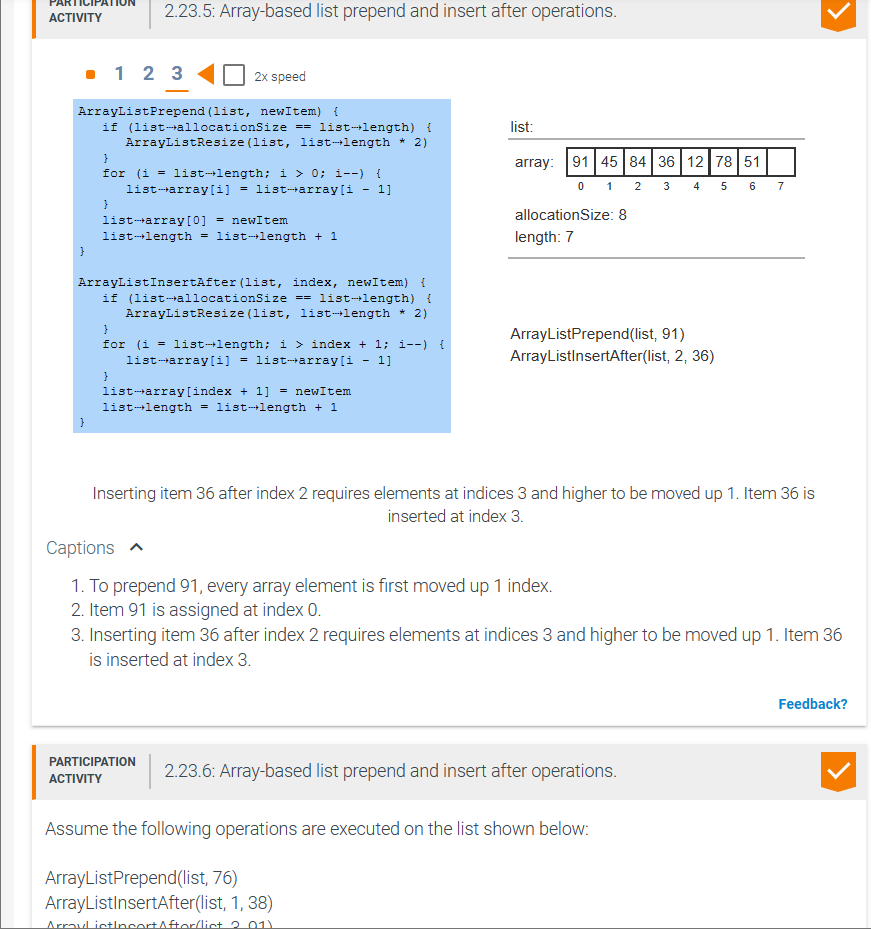
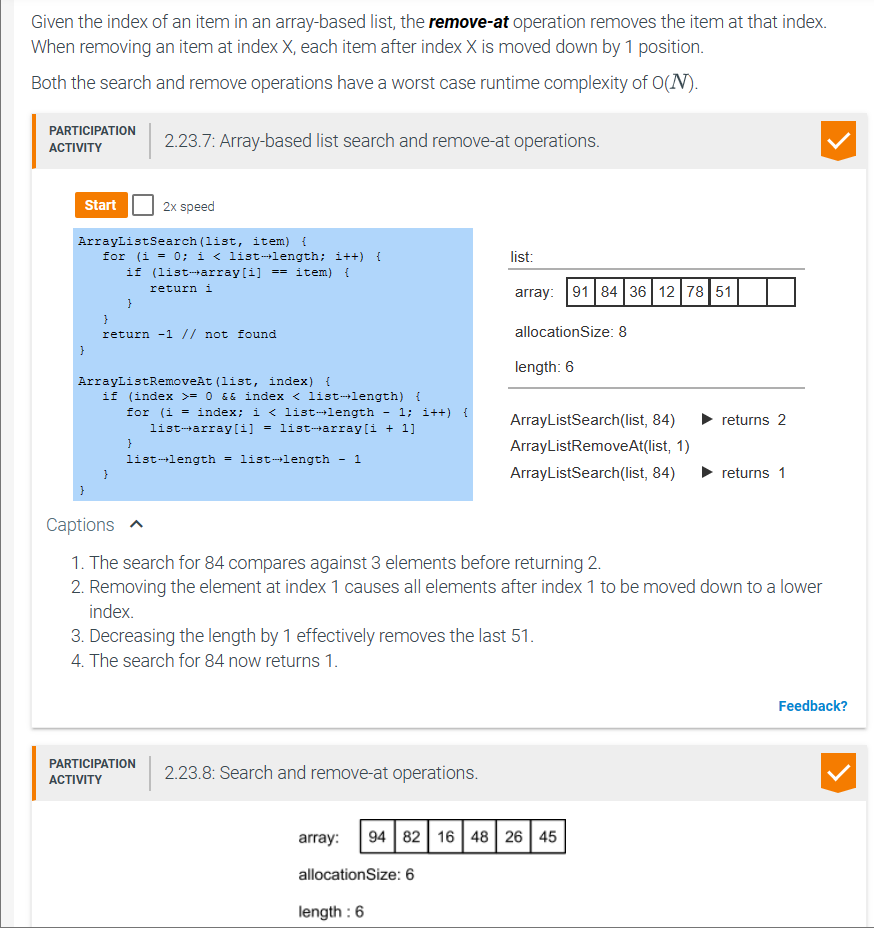
An array-based list must be resized if an item is added when the allocation size equals the list length. A new array is allocated with a length greater than the existing array. Allocating the new array with twice the current length is a common approach. The existing array elements are then copied to the new array, which becomes the list's storage array. Because all existing elements must be copied from 1 array to another, the resize operation has a runtime complexity of O(N). ArrayListAppend(list, 51) 51 can now be appended to the array. Captions 1. The allocation size and length of the list are both 4 . An append operation cannot add to the existing array. 2. To resize, a new array is allocated of size 8 , and the existing elements are copied to the new array. The new array replaces the list's array. 3. 51 can now be appended to the array. list: array: allocationSize: 8 length: 7 Inserting item 36 after index 2 requires elements at indices 3 and higher to be moved up 1. Item 36 is inserted at index 3. 1. To prepend 91 , every array element is first moved up 1 index. 2. Item 91 is assigned at index 0. 3. Inserting item 36 after index 2 requires elements at indices 3 and higher to be moved up 1. Item 36 is inserted at index 3. 2.23.6: Array-based list prepend and insert after operations. Assume the following operations are executed on the list shown below: ArrayListPrepend(list, 76) ArrayListInsertAfter(list, 1, 38) Given the index of an item in an array-based list, the remove-at operation removes the item at that index. When removing an item at index X, each item after index X is moved down by 1 position. Both the search and remove operations have a worst case runtime complexity of O(N). \begin{tabular}{l|l} PARTICIPATION & 2.23.7: Array-based list search and remove-at operations. \\ ACTIVITY & \end{tabular} Captions 1. The search for 84 compares against 3 elements before returning 2. 2. Removing the element at index 1 causes all elements after index 1 to be moved down to a lower index. 3. Decreasing the length by 1 effectively removes the last 51. 4. The search for 84 now returns 1