cannot use user-defined functions besides int main(void). written in c code. thank you

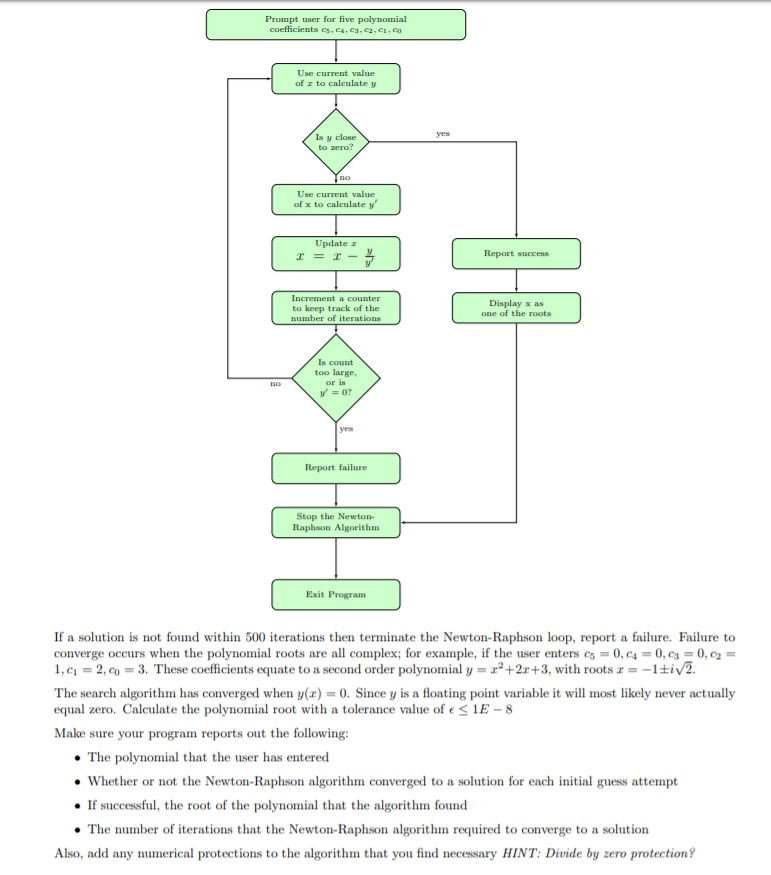
2 Polynomial Root Calculation: Problem Description (30 points) Engineers often need to calculate the roots to a given polynomial. For low order polynomials these computations can be done by hand. For higher order polynomials these calculations can be cumbersome, if not impossible, without a computer. One method of finding real roots of a polynomial is the Newton-Raphson algorithm. In this homework we will write a program that uses the Newton-Raphson method for calculating the roots of a polynomial. Although our program will not be able to solve for complex roots, it will be able to calculate real roots; maybe later we will upgrade the routine to include complex roots. Since it is possible that the polynomial roots are all complex, i.e. no real roots at all, or it may be that the Newton-Raphson routine fails to converge. 2.1 Newton-Raphson Algorithm: Write a program that prompts the user to input the coefficients C5, C4, C3, C2,C1,Co of a 5th-order polynomial. The 5th order polynomial has the form y=052 +04:24 +03:23 +022+61 2+co We know that the first derivative of y with respect to zis = y' = 5.05.2* +4.04.23 +3.03.12 +2.02.2+1 We can use this information to find the roots of the polynomial. The basic idea, in the Newton-Raphson method, is as follows: (a) Given an initial guess x, and polynomial coefficients c, calculate y (b) Check to see if y is close enough to zero, i.e. within some small tolerance close to zero. (i) If so then terminate. Algorithm has converged! (ii) If not then continue (c) Use the current value of x to calculate y' (d) Create a new guess for x using the update formula x = (e) Increment a counter to count the number of algorithm iterations (f) Check to see if the number of iterations has exceeded a predetermined count limit (say 500) (i) If so then terminate. Algorithm has failed! (ii) If not then return to step a This same information is described in the flow chart below: Prompt user for five polynomial coefficients , 4.c3.. . 0 Use current value of to calculate y Is y close to zero? Use current value of x to calculate w Update = 2 - Report success Increment a counter to keep track of the number of iterations Display xas one of the roots Is count too large, or is y = Report failure Stop the Newton Raphson Algorithm Exit Program If a solution is not found within 500 iterations then terminate the Newton-Raphson loop, report a failure. Failure to converge occurs when the polynomial roots are all complex; for example, if the user enters as = 0,4 = 0,03 = 0,2 = 1, C = 2, co = 3. These coefficients equate to a second order polynomial y = x+2x+3, with roots 2 = -1+iv2. The search algorithm has converged when y(x) = 0. Since y is a floating point variable it will most likely never actually equal zero. Calculate the polynomial root with a tolerance value of