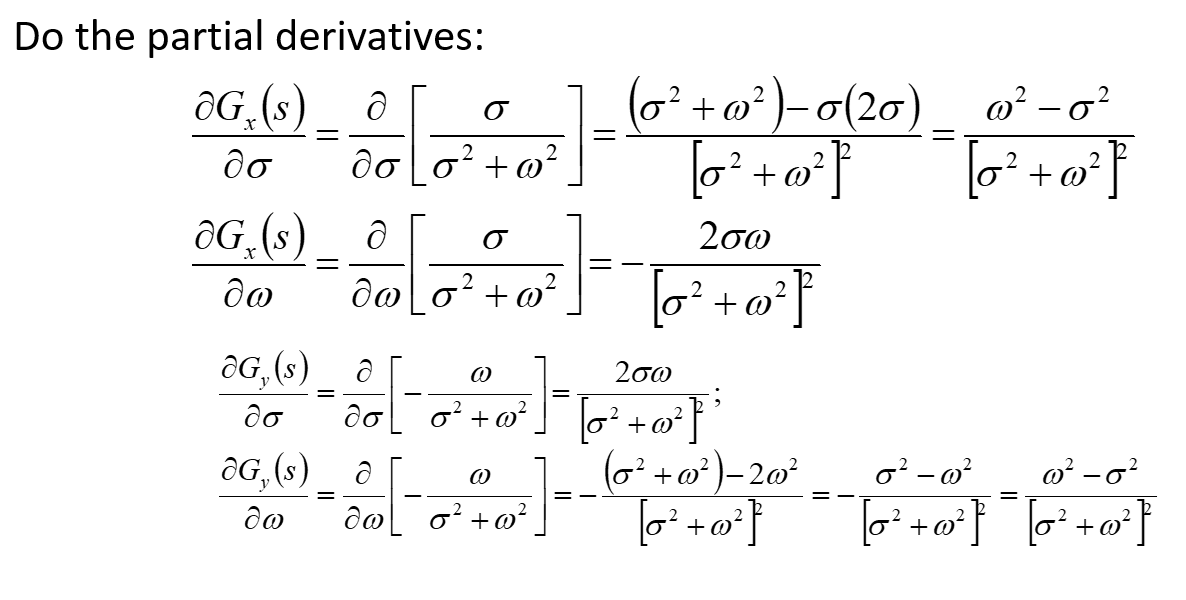
Cauchy-Riemann Condition (cont.) Rewrite it in a more convenient form: G(s)= 1 S = 1 - j@ = - j@ 2 +j(+ja)( jw)o + w Identify the real and imaginary components: G(s) = G(s)+ jG,(s)= 2 + w G(s)= ; G. 2 2" and G,(s)= 2 jo + w @ 2 2 Do the partial derivatives: G (s) a G(s) = ( + w)-(20)_ @ o 0001000000+0] do do 2 G(s)_ a = 2 dwo + w AG,(s) a = 2 [o + w ] @ 2 [o @ + (0+0)-20 [o + w } } OG, (s) G(s) a 0+00 [[o + m ] [o + w } Now, compare the conditions! OG(s) w - Gy G (s) do 2 [o + a } 2 G(s) 2 OG (s) 2 and [ + w } } do [o + w ]} } The Cauchy-Riemann condition holds and hence, the function is analytical! Cauchy-Riemann: Analytical function Homework problem #1: Verify if the Cauchy-Riemann condition is satisfied for the following analytical function ! 1 G(s) = S+1 Cauchy-Riemann Condition (cont.) Example Problem on Cauchy-Riemann condition for analyticity and linearity: Given example problem: 1 G(s) = where: s=+ j@ S , Demonstrate if Cauchy-Riemann condition holds!