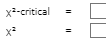(Ch 15-EOC-Q1-3)Please answer all questions. Note: For the first blank in Question 3 (to complete the sentence), the answer options are "are no" or "are". For the last blank in the sentence the answer options are: "k=4"/ "p<.05>.05". All the other blue blank spots require numerical computations/data to complete the sentence correctly.

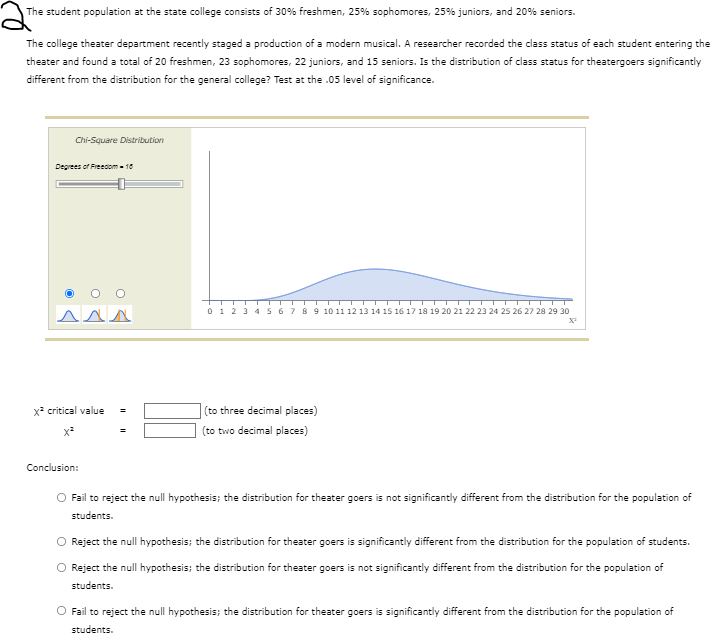
Parametric tests (such as t or ANOVA) differ from nonparametric tests (such as chi-square) primarily in terms of the assumptions they require and the data they use. Which of the following are true about nonparametric tests? Check all that apply. Nonparametric tests do not require the populations to have normal distributions. Nonparametric tests require data measured on an interval or ratio scale. Nonparametric tests require the populations to satisfy numerous assumptions. Nonparametric tests can be performed on data measured on any scale. Nonparametric tests make few, if any, assumptions about the populations. Nonparametric tests require different populations to have equal variances.Do the data indicate any significant preferences among the four colors? Test at the .05 level of significance. (Round your answers to two decimal places for x2-critical and x2.)\fThe student population at the state college consists of 30% freshmen, 25% sophomores, 25% juniors, and 20% seniors. The college theater department recently staged a production of a modern musical. A researcher recorded the class status of each student entering the theater and found a total of 20 freshmen, 23 sophomores, 22 juniors, and 15 seniors. Is the distribution of class status for theatergoers significantly different from the distribution for the general college? Test at the .05 level of significance. Chi-Square Distribution Degrees of Freedom - 18 O O O AAA 8 12 385 6 18 9 10 11 12 13 14 15 16 17 19 19 20 21 2 23 24 25 26 27 28 29 30 x3 critical value = (to three decimal places) (to two decimal places) Conclusion: O Fail to reject the null hypothesis; the distribution for theater goers is not significantly different from the distribution for the population of students. O Reject the null hypothesis; the distribution for theater goers is significantly different from the distribution for the population of students. O Reject the null hypothesis; the distribution for theater goers is not significantly different from the distribution for the population of students. O Fail to reject the null hypothesis; the distribution for theater goers is significantly different from the distribution for the population of students.Conclusion: O Fail to reject null hypothesis. There are no preferences among the four colors. O Reject null hypothesis. There are preferences among the four colors. O Reject null hypothesis. There are no preferences among the four colors. O Fail to reject null hypothesis. There are preferences among the four colors. Complete the following sentence demonstrating how the outcome of the hypothesis test would appear in a research report. The results of the chi-square test indicate that there significant preferences among the four colors, x?( # , N = ) =A developmental psychologist would like to determine whether infants display any color preferences. A stimulus consisting of four color patches (red, green, blue, and yellow) is projected onto the ceiling above a crib. Infants are placed in the crib, one at a time, and the psychologist records how much time each infant spends looking at each of the four colors. The color that receives the most attention during a 100-second test period is identified as the preferred color for that infant. The preferred colors for a sample of 80 infants are shown in the following table