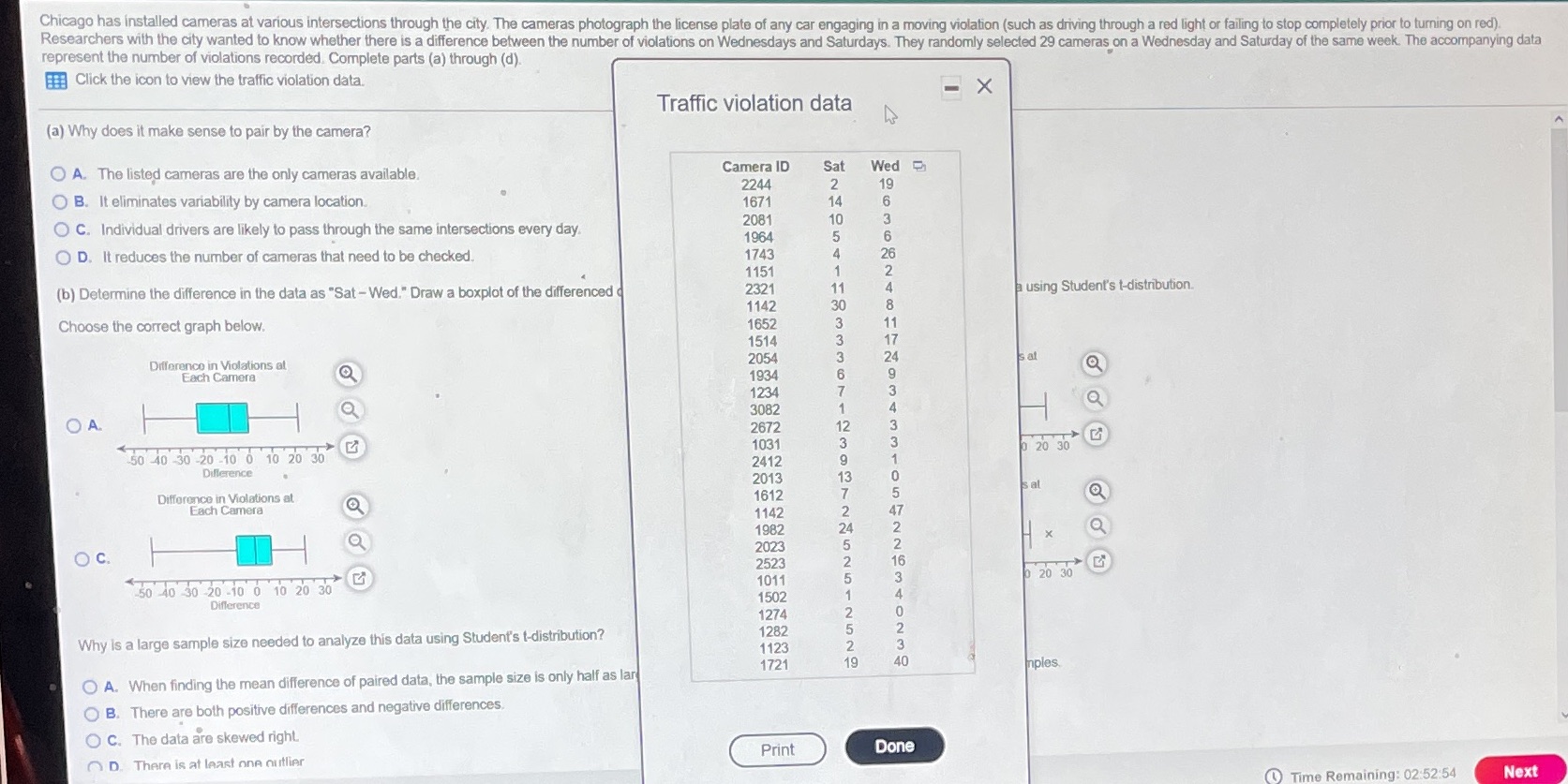
Chicago has installed cameras at various intersections through the city. The cameras photograph the license plate of any car engaging in a moving violation (such as driving through a red light or failing to stop completely prior to turning on red) Researchers with the city wanted to know whether there is a difference between the number of violations on Wednesdays and Saturdays. They randomly selected 29 cameras on a Wednesday and Saturday of the same week. The accompanying data represent the number of violations recorded. Complete parts (a) through (d). Click the icon to view the traffic violation data. X Traffic violation data (a) Why does it make sense to pair by the camera? A. The listed cameras are the only cameras available. Camera ID Sat Wed 2244 2 19 O B. It eliminates variability by camera location. 1671 14 6 10 3 O C. Individual drivers are likely to pass through the same intersections every day. 2081 1964 5 6 O D. It reduces the number of cameras that need to be checked. 1743 4 26 1151 1 (b) Determine the difference in the data as "Sat -Wed." Draw a boxplot of the differenced 2321 11 using Student's t-distribution. 1142 30 Choose the correct graph below. 1652 1514 2054 sat Difference in Violations at Each Camera 1934 1234 3082 O A. 2672 1031 20 30 50 40 30 20 10 0 10 20 30 2412 Difference 2013 SWNOAWONNACO- WWAWONTO Sa CONUN-UNGENSHOWN- NOWWW Difference in Violations at 1612 Each Camera 1142 1982 X O c. 2023 2523 50 40 30 20 -10 0 10 20 30 1011 20 30 Difference 1502 1274 Why is a large sample size needed to analyze this data using Student's t-distribution? 1282 1123 1721 nples O A. When finding the mean difference of paired data, the sample size is only half as lar O B. There are both positive differences and negative differences, O C. The data are skewed right. Print Done D. There is at least one outlier Time Remaining: 02:52:54 Nextbution has les of freedom inc Chicago has installed cameras at various intersections through the city. The cameras photograph the license plate of any car engaging in a moving violation (such increases, s b as driving through a red light or failing to stop completely prior to turning on red). Researchers with the city wanted to know whether there is a difference between the number of violations on Wednesdays and Saturdays. They randomly selected 29 cameras on a Wednesday and Saturday of the same week. The accompanying a by the law data represent the number of violations recorded. Complete parts (a) through (d). Click the icon to view the traffic violation data. O A. When finding the mean difference of paired data, the sample size is only half as large as finding the difference of means between two independent samples. e size h increa O B. There are both positive differences and negative differences. of t gets clos O C. The data are skewed right. mal density cu O D. There is at least one outlier. oduced Into t(c) Does the sample evidence suggest there is a difference in the number of violations on a Wednesday versus Saturday? Use a = 0.05. Determine the null and alternative hypotheses. Ho : Hd H1 : Hd (Type integers or decimals. Do not round.) Determine the test statistic. The test statistic is (Round to two decimal places as needed.) Determine the P-value. The P-value is. (Round to three decimal places as needed.) notarming the nrnar ronellicion foccurs if the(Round to two decimal places as needed.) Determine the P-value. The P-value is (Round to three decimal places as needed.) Determine the proper conclusion. Ho. There sufficient evidence to conclude that the number of Wednesday violations is the number of Saturday violations. (d) What other variables may confound the results of the study? Select all that apply. A. Whether or not school is in session B. Weather C. Camera model D. Car color E. Time of day F. There is no risk of confounding in this study. le Time Remaining: 02:17:05 Next er Statcrunch TVi