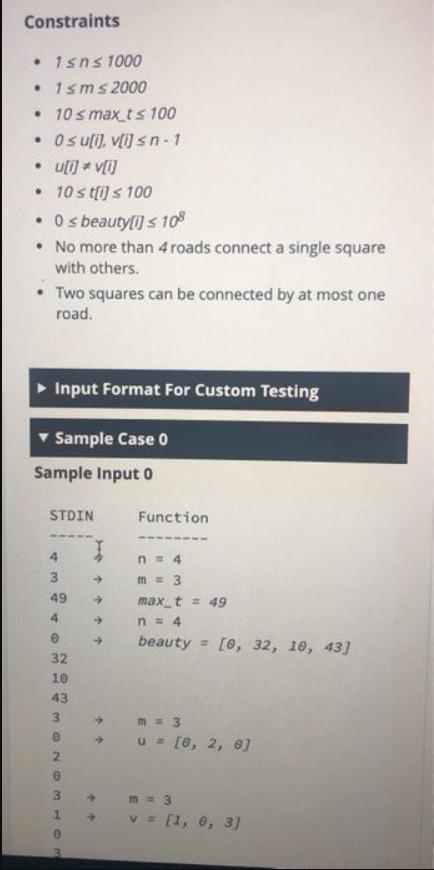
You have just arrived in a new city and would like to see its sights. Each sight is located in a square and you have assigned each a beauty value. Each road to a square takes an amount of time to travel, and you have limited time for sightseeing. Determine the maximum value of beauty that you can visit during your time in the city. Start and finish at your hotel, the location of sight zero. Example n = 4 m = 3 %3! max_t = 50 beauty [5, 10, 15, 20] u = [0, 1, 0] v [1, 2, 3] t= [10, 10, 10] n=4 squares are chosen in the map, including the hotel at square 0. m= 3 bidirectional roads that connect them Edges are between squares uf] and vfi), and t [] is the time to travel edge i beauty = (5, 10, 15, 20] represents the beauty values for squares 0, 1, 2, and 3 respectively. To visit Square 0, 1 and 2 (Starting at the hotel and ending at the hotel), it takes 10 + 10 + 10 + 10 = 40 minutes and it has 5+ 10 + 15 30 beauty value (the beauty value is counted only on your first visit.) To do a round trip from square 0 to square 3, it hackerrank.com/test/7tb6ldm4ljb/questions/c29hpks40a 20= %3D To do a round trip from square 0 to square 3, it takes 10 + 10 -20 minutes and it has only 5+ 20%3D 25 beauty value. The path that gathers squares with the maximum value of beauty that you can visit during max_t= 50 minutes or less, is squares = [0, 1, 2] with 30 as a beauty value. 10 1/10 2/15 10 0/5 10 3/20 Function Description Complete the function findBestPath in the editor below. findBestPath has the following parameter(s): int r. an integer, the number of sights in the city int m. an integer, the number of connecting roads int max t an integer, the amount of time for sightseeing int beauty[n). integer array, the beauty values you have assigned to each sight int u[m) integer array, the starting sight location for each bidirectional road int v[m). integer array, the ending sight location for each bidirectional road int t[m): integer array, the travel time for each bidirectional road Returns: int an integer, the maximum sum of beauty Constraints 1sns 1000 1sms2000 10 s max_t s 100 O s uli]), v[i] sn-1 uli] * v[i] 10 s ti] s 100 Os beauty[i) s 108 No more than 4 roads connect a single square with others. Two squares can be connected by at most one road. Input Format For Custom Testing Sample Case 0 Sample Input O STDIN Function 4 n = 4 3. m = 3 49 max t = 49 4. n = 4 beauty = [0, 32, 10, 43] 32 10 43 3. m = 3 [8, 2, 6] 3. m= 3 V= [1, e, 3]