Clearlysolvethefollowingquestions: Question.,

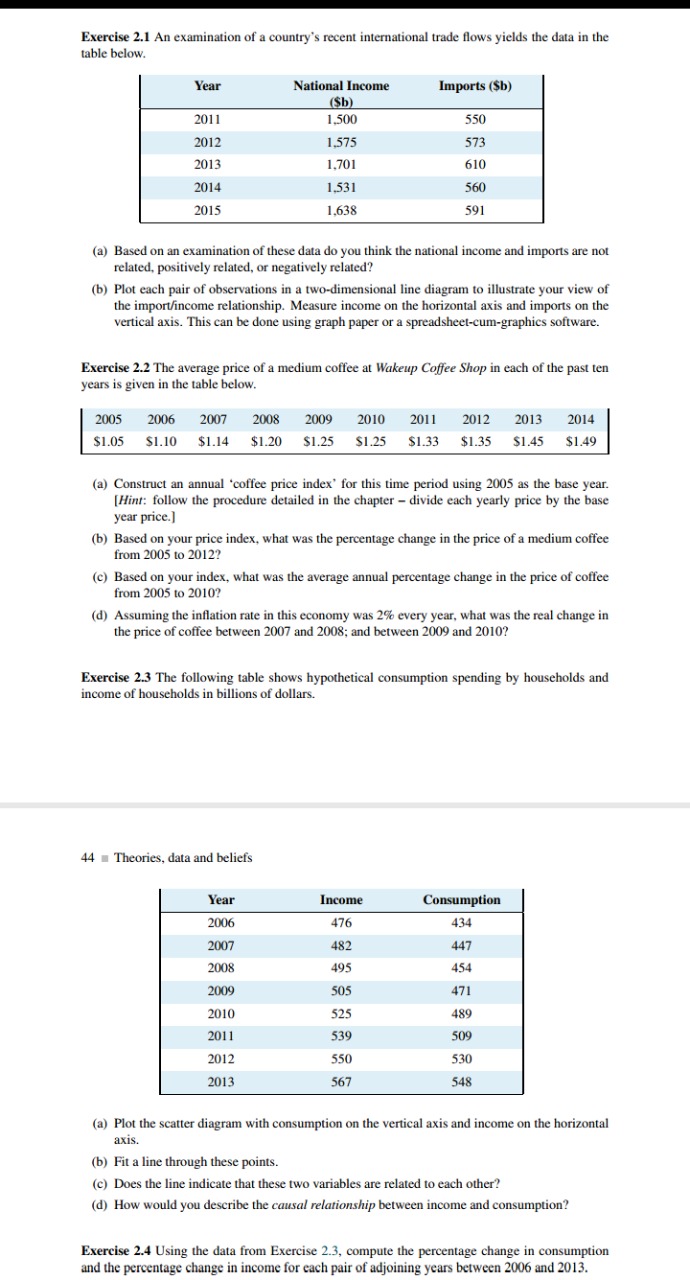
The random variable Y is defined by: N Y =>X; 1=1 where the X,'s are independent Bin(n, p) random variables and N is a Poisson random variable, independent of the X; 's, with mean 1. (i) Prove from first principles that the moment generating function of Y is given by: My(1) = exp a[(q + pe')"-1] [4] (ii) Hence derive expressions for the mean and variance of Y . [4] [Total 8]Exercise 2.1 An examination of a country's recent international trade flows yields the data in the table below. Year National Income Imports ($b) ($b) 2011 1,500 550 2012 1,575 573 2013 1.701 610 2014 1,531 560 2015 1,638 591 (a) Based on an examination of these data do you think the national income and imports are not related, positively related, or negatively related? (b) Plot each pair of observations in a two-dimensional line diagram to illustrate your view of the import/income relationship. Measure income on the horizontal axis and imports on the vertical axis. This can be done using graph paper or a spreadsheet-cum-graphics software. Exercise 2.2 The average price of a medium coffee at Wakeup Coffee Shop in each of the past ten years is given in the table below. 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 $1.05 $1.10 $1.14 $1.20 $1.25 $1.25 $1.33 $1.35 $1.45 $1.49 (a) Construct an annual "coffee price index' for this time period using 2005 as the base year. [Hint: follow the procedure detailed in the chapter - divide each yearly price by the base year price.] (b) Based on your price index, what was the percentage change in the price of a medium coffee from 2005 to 2012? (c) Based on your index, what was the average annual percentage change in the price of coffee from 2005 to 2010? (d) Assuming the inflation rate in this economy was 2% every year, what was the real change in the price of coffee between 2007 and 2008; and between 2009 and 2010? Exercise 2.3 The following table shows hypothetical consumption spending by households and income of households in billions of dollars. 44 . Theories, data and beliefs Year Income Consumption 2006 476 434 2007 482 447 2008 495 454 2009 505 471 2010 525 489 2011 539 509 2012 550 530 2013 567 548 (a) Plot the scatter diagram with consumption on the vertical axis and income on the horizontal axis. (b) Fit a line through these points. (c) Does the line indicate that these two variables are related to each other? (d) How would you describe the causal relationship between income and consumption? Exercise 2.4 Using the data from Exercise 2.3, compute the percentage change in consumption and the percentage change in income for each pair of adjoining years between 2006 and 2013.EXERCISES FOR CHAPTER 1 Exercise 1.1 An economy has 100 identical workers. Each one can produce four cakes or three shirts, regardless of the number of other individuals producing each good. (a) How many cakes can be produced in this economy when all the workers are cooking? (b) How many shirts can be produced in this economy when all the workers are sewing? (c) On a diagram with cakes on the vertical axis, and shirts on the horizontal axis, join these points with a straight line to form the PPF. (d) Label the inefficient and unattainable regions on the diagram. Exercise 1.2 In the table below are listed a series of points that define an economy's production possibility frontier for goods Y and X. Y 1000 900 800 700 600 500 400 300 200 100 0 X 0 1600 2500 3300 4000 4600 5100 5500 5750 5900 6000 (a) Plot these pairs of points to scale, on graph paper, or with the help of a spreadsheet. (b) Given the shape of this PPF is the economy made up of individuals who are similar or different in their production capabilities (c) What is the opportunity cost of producing 100 more Y at the combination (X = 5500, Y = 300). (d) Suppose next there is technological change so that at every output level of good Y' the econ- omy can produce 20 percent more X. Enter a new row in the table containing the new values, and plot the new PPF. Exercise 1.3 Using the PPF that you have graphed using the data in Exercise 1.2, determine if the following combinations are attainable or not: (X = 3000, Y = 720), (X = 4800, Y = 480). Exercise 1.4 You and your partner are highly efficient people. You can earn $20 per hour in the workplace; your partner can earn $30 per hour. (a) What is the opportunity cost of one hour of leisure for you? (b) What is the opportunity cost of one hour of leisure for your partner? (c) Now consider what a PPF would look like: You can produce/consume two things, leisure and income. Since income buys things you can think of the PF as having these two 'prod- ucts' - leisure and consumption goods/services. So, with leisure on the horizontal axis and income in dollars is on the vertical axis, plot your PPF. You can assume that you have 12 Exercises for Chapter 1 = 27 hours per day to allocate to either leisure or income. [Hint: the leisure axis will have an intercept of 12 hours. The income intercept will have a dollar value corresponding to where all hours are devoted to work.] (d) Draw the PPF for your partner. Exercise 1.5 Louis and Carrie Anne are students who have set up a summer business in their neighbourhood. They cut lawns and clean cars. Louis is particularly efficient at cutting the grass - he requires one hour to cut a typical lawn, while Carrie Anne needs one and one half hours. In contrast, Carrie Anne can wash a car in a half hour, while Louis requires three quarters of an hour. (a) If they decide to specialize in the tasks, who should cut the grass and who should wash cars? (b) If they each work a twelve hour day, how many lawns can they cut and how many cars can they wash if they each specialize in performing the task where they are most efficient? (c) Illustrate the PPF for each individual where lawns are on the horizontal axis and car washes on the vertical axis, if each individual has twelve hours in a day.1 Let # ~binomial(N, q), where q is unknown and A is large. Using the fact that the posterior distribution of q is approximately N(q, V), where V = d2 -1 doz (log D)(4) find a formula for an approximate 95% Bayesian confidence interval for q. 2 The following table gives the exposed to risk, Exo, and deaths 640, for certain male and female tuberculosis patients in Sweden: exposed to risk deaths males 221 68 females 194 83 Test, at the 1% significance level, the hypothesis that the true rate of mortality at age 40 is the same for both sexes. 3 The following data refer to surrenders among the holders of three types of life assurance contract (mortality being ignored.) No. of policies in force No. of surrenders Policy type on 1 January 2000 in 2000 A 2,489 167 B 1,524 93 C 3,002 173 Test the hypothesis that the true surrender rates are the same for all 3 types of contract