
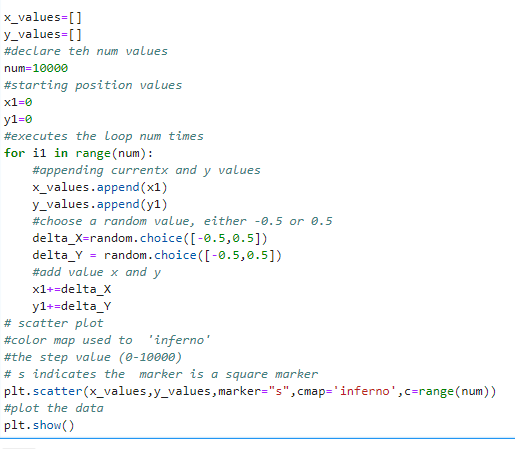
 Code for walk
Code for walk
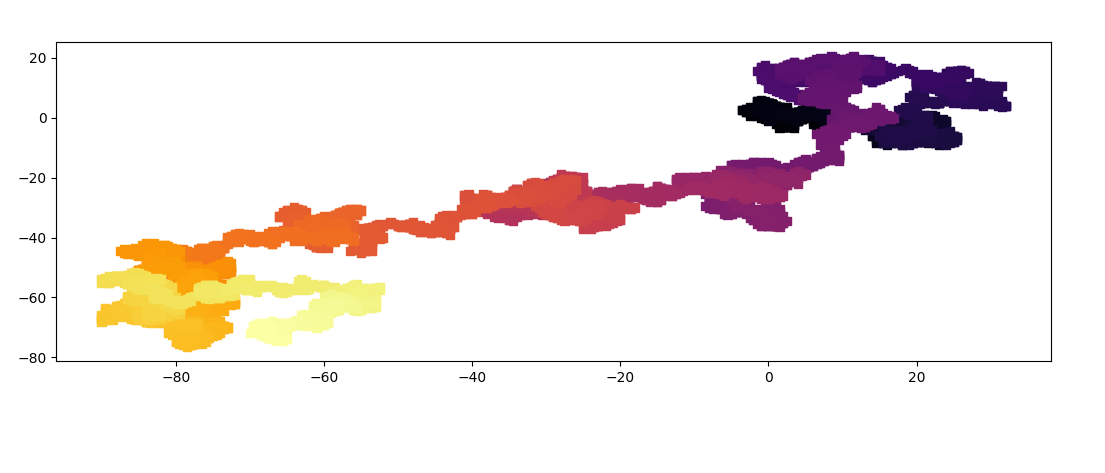
2.2 Make nwalk = 1000 walks of n = 10000 steps. For each walk, save an array with the Euclidean distance between the origin and each of the n positions. After you have performed all of the random walks, plot a histogram of the maximum distance and final distance of the walks on the same diagram, using the alpha option to make both histograms semi- transparent so they both can be seen. Create a line plot of the distance vs. step number for every 100th random-walk combined. Each walk should be its own line. 2.3 Explore the maximum distance the random walk gets away from the origin as a function of the number of steps taken. Make n = 2 steps for p = [4, 5, ..., 13), and each time make nwalk = 1000 walks to establish good statistics. For each of the 10 cases (one for each p) determine the distance Imax-hist at which the maximum of the histogram of the maximum distance of the nwalk walks for this case with n steps is located. Then plot Imax-hist vs. logion. X_values=[] y_values=[] #declare teh num values num=10000 #starting position values x1=0 y1=0 #executes the Loop num times for il in range(num): #appending currentx and y values X_values.append(x1) y_values.append(yi) #choose a random value, either -0.5 or 0.5 delta_X=random.choice([-0.5,0.5]) delta_Y = random.choice([-0.5, 0.5]) #add value x and y x1+=delta_x yl+=delta_Y # scatter plot #color map used to 'inferno' #the step value (0-10000) # s indicates the marker is a square marker plt. scatter(x_values,y_values, marker="5",cmap='inferno',c=range(num)) #plot the data plt.show() -60 -40 -20 2.2 Make nwalk = 1000 walks of n = 10000 steps. For each walk, save an array with the Euclidean distance between the origin and each of the n positions. After you have performed all of the random walks, plot a histogram of the maximum distance and final distance of the walks on the same diagram, using the alpha option to make both histograms semi- transparent so they both can be seen. Create a line plot of the distance vs. step number for every 100th random-walk combined. Each walk should be its own line. 2.3 Explore the maximum distance the random walk gets away from the origin as a function of the number of steps taken. Make n = 2 steps for p = [4, 5, ..., 13), and each time make nwalk = 1000 walks to establish good statistics. For each of the 10 cases (one for each p) determine the distance Imax-hist at which the maximum of the histogram of the maximum distance of the nwalk walks for this case with n steps is located. Then plot Imax-hist vs. logion. X_values=[] y_values=[] #declare teh num values num=10000 #starting position values x1=0 y1=0 #executes the Loop num times for il in range(num): #appending currentx and y values X_values.append(x1) y_values.append(yi) #choose a random value, either -0.5 or 0.5 delta_X=random.choice([-0.5,0.5]) delta_Y = random.choice([-0.5, 0.5]) #add value x and y x1+=delta_x yl+=delta_Y # scatter plot #color map used to 'inferno' #the step value (0-10000) # s indicates the marker is a square marker plt. scatter(x_values,y_values, marker="5",cmap='inferno',c=range(num)) #plot the data plt.show() -60 -40 -20

 Code for walk
Code for walk






