code in c#:
public class SearchingAndSorting { // This is from a prior exercise. // If you havent done it yet, you should it // just prints out everything in the nums array public void printArray(int[] nums) { // Your code goes here. }
public bool FindIntegerLinear(int target, int[] array) { // Your code goes here. return false; }
public bool FindIntegerBinary(int target, int[] array) { return false; }
public bool FindIntegerBinaryRecursive(int target, int[] array) { FindIntegerBinaryRecursive(target, array, 0, array.Length - 1); return false; }
private bool FindIntegerBinaryRecursive(int target, int[] array, int lowestIndex, int highestIndex) { FindIntegerBinaryRecursive(target, array, lowestIndex + 1, highestIndex - 1); return false; }
public bool FindIntegerLinearPerfMeasured(int target, int[] array, out int numComparisons) { // Your code goes here. numComparisons = 0; return false; }
public bool FindIntegerBinaryPerfMeasured(int target, int[] array, out int numComparisons) { numComparisons = 0; return false; }
public void BubbleSort(int[] nums) { }
public void BubbleSortPerfMeasured(int[] nums, out int numSwaps, out int numComparisons) { numSwaps = numComparisons = 0; } }
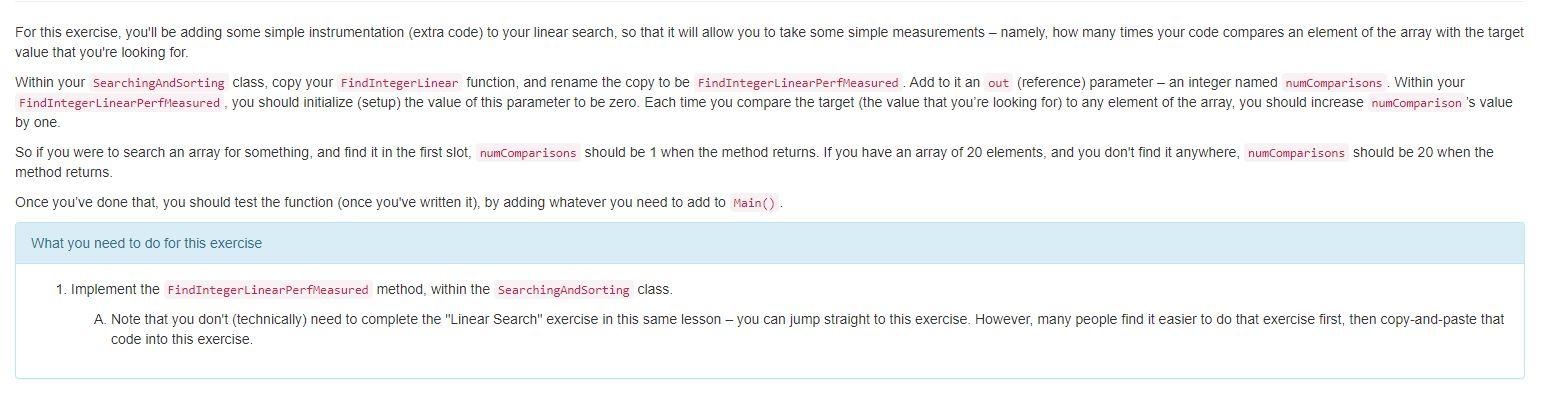
For this exercise, you'll be adding some simple instrumentation (extra code) to your linear search, so that it will allow you to take some simple measurements - namely, how many times your code compares an element of the array with the target value that you're looking for. Within your searchingAndSorting class, copy your FindIntegerLinear function, and rename the copy to be FindIntegerLinearPerfMeasured. Add to it an out (reference) parameter - an integer named numcomparisons. Within your FindIntegerLinearPerfileasured, you should initialize (setup) the value of this parameter to be zero. Each time you compare the target (the value that you're looking for) to any element of the array, you should increase numcomparison's value by one So if you were to search an array for something, and find it in the first slot, numComparisons should be 1 when the method returns. If you have an array of 20 elements, and you don't find it anywhere, numComparisons should be 20 when the method returns Once you've done that, you should test the function (once you've written it), by adding whatever you need to add to Main(). What you need to do for this exercise 1. Implement the FindIntegerLinearPerfMeasured method, within the searchingAndSorting class. A. Note that you don't (technically) need to complete the "Linear Search" exercise in this same lesson - you can jump straight to this exercise. However, many people find it easier to do that exercise first, then copy-and-paste that code into this exercise. For this exercise, you'll be adding some simple instrumentation (extra code) to your linear search, so that it will allow you to take some simple measurements - namely, how many times your code compares an element of the array with the target value that you're looking for. Within your searchingAndSorting class, copy your FindIntegerLinear function, and rename the copy to be FindIntegerLinearPerfMeasured. Add to it an out (reference) parameter - an integer named numcomparisons. Within your FindIntegerLinearPerfileasured, you should initialize (setup) the value of this parameter to be zero. Each time you compare the target (the value that you're looking for) to any element of the array, you should increase numcomparison's value by one So if you were to search an array for something, and find it in the first slot, numComparisons should be 1 when the method returns. If you have an array of 20 elements, and you don't find it anywhere, numComparisons should be 20 when the method returns Once you've done that, you should test the function (once you've written it), by adding whatever you need to add to Main(). What you need to do for this exercise 1. Implement the FindIntegerLinearPerfMeasured method, within the searchingAndSorting class. A. Note that you don't (technically) need to complete the "Linear Search" exercise in this same lesson - you can jump straight to this exercise. However, many people find it easier to do that exercise first, then copy-and-paste that code into this exercise







