Combinations and Permutations (Show full working please!)

QUESTIONS:

1. Decide if the situation involves permutations, combinations, or neither.

The number of ways you can choose 2 books from a selection of 8 to bring on vacation

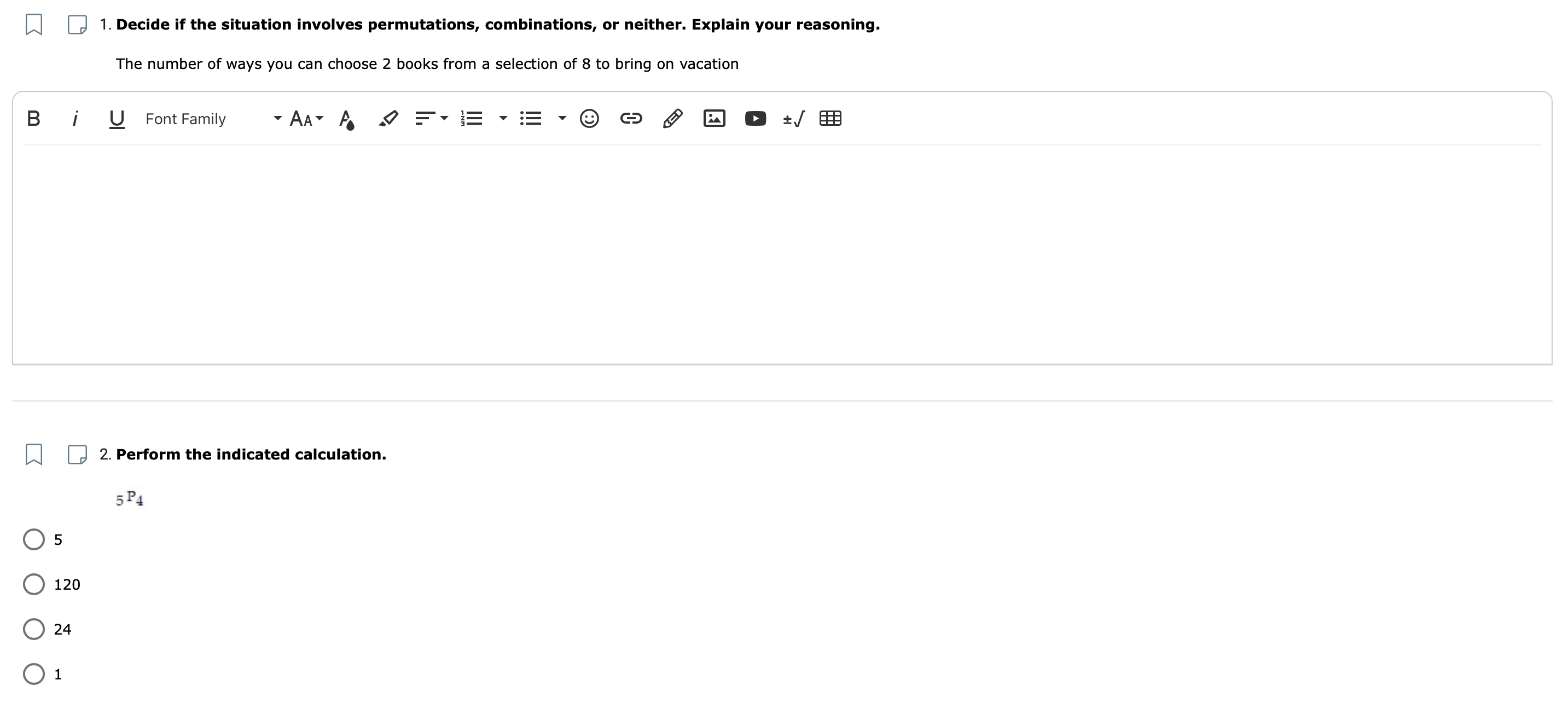
2. Perform the indicated calculation. Explain reasoning.

5^P4

a) 5

b) 120

c) 24

d) 1

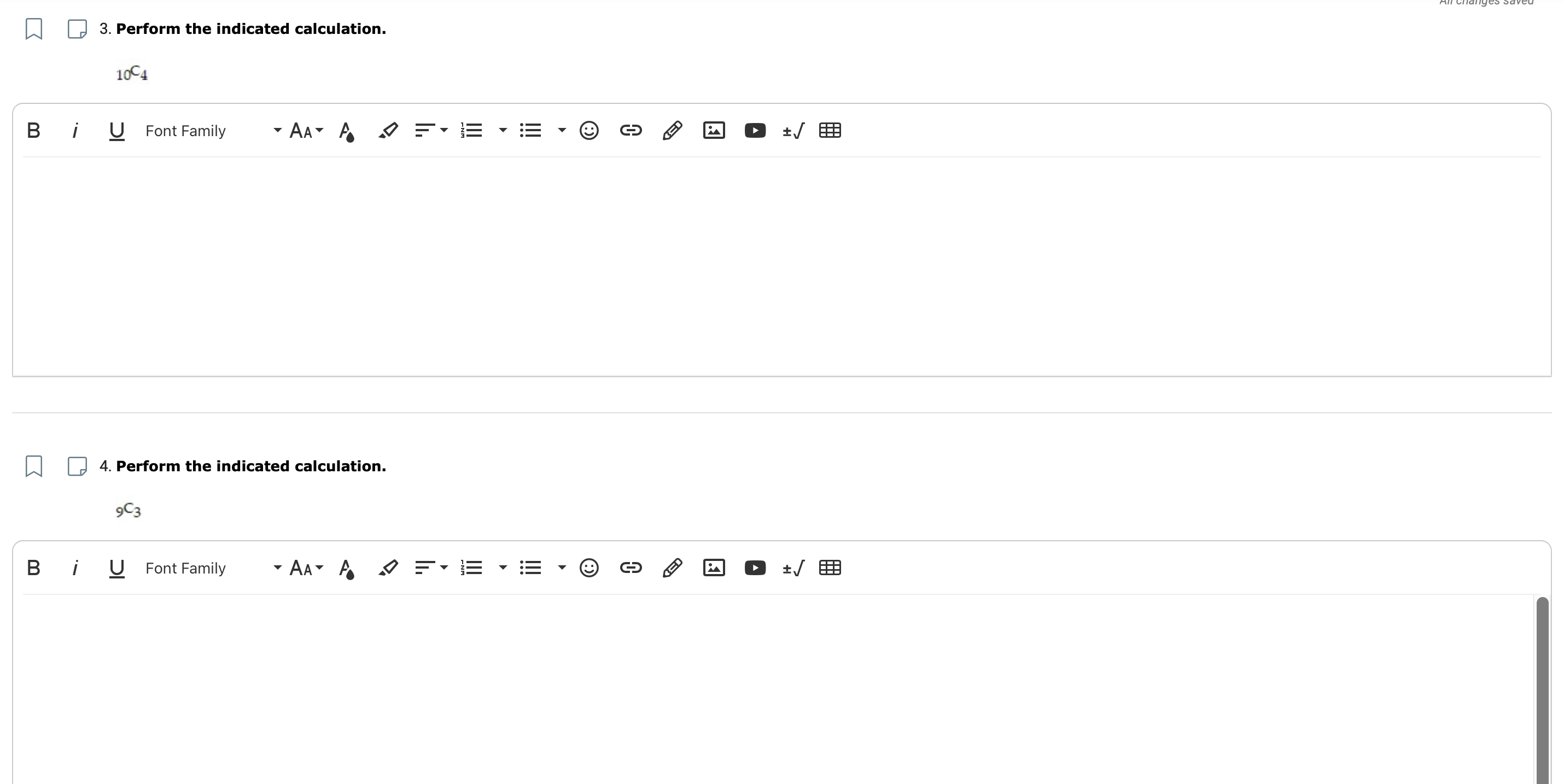
3. Perform the indicated calculation

10^C4

4. Perform the indicated calculation

9^C3

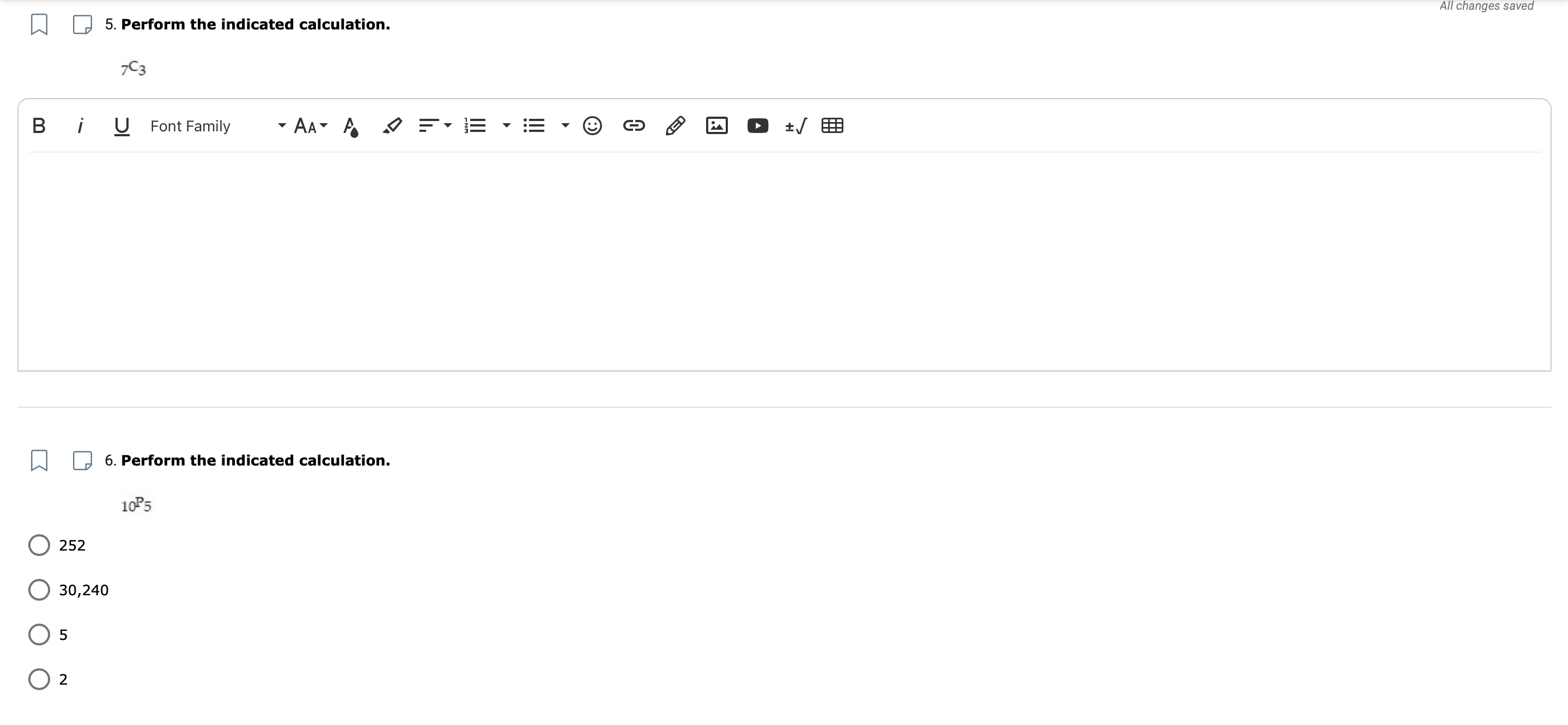
5. Perform the indicated calculation

7^C3

6. Perform the indicated calculation

10^P5

a) 252

b) 30,240

c) 5

d) 2

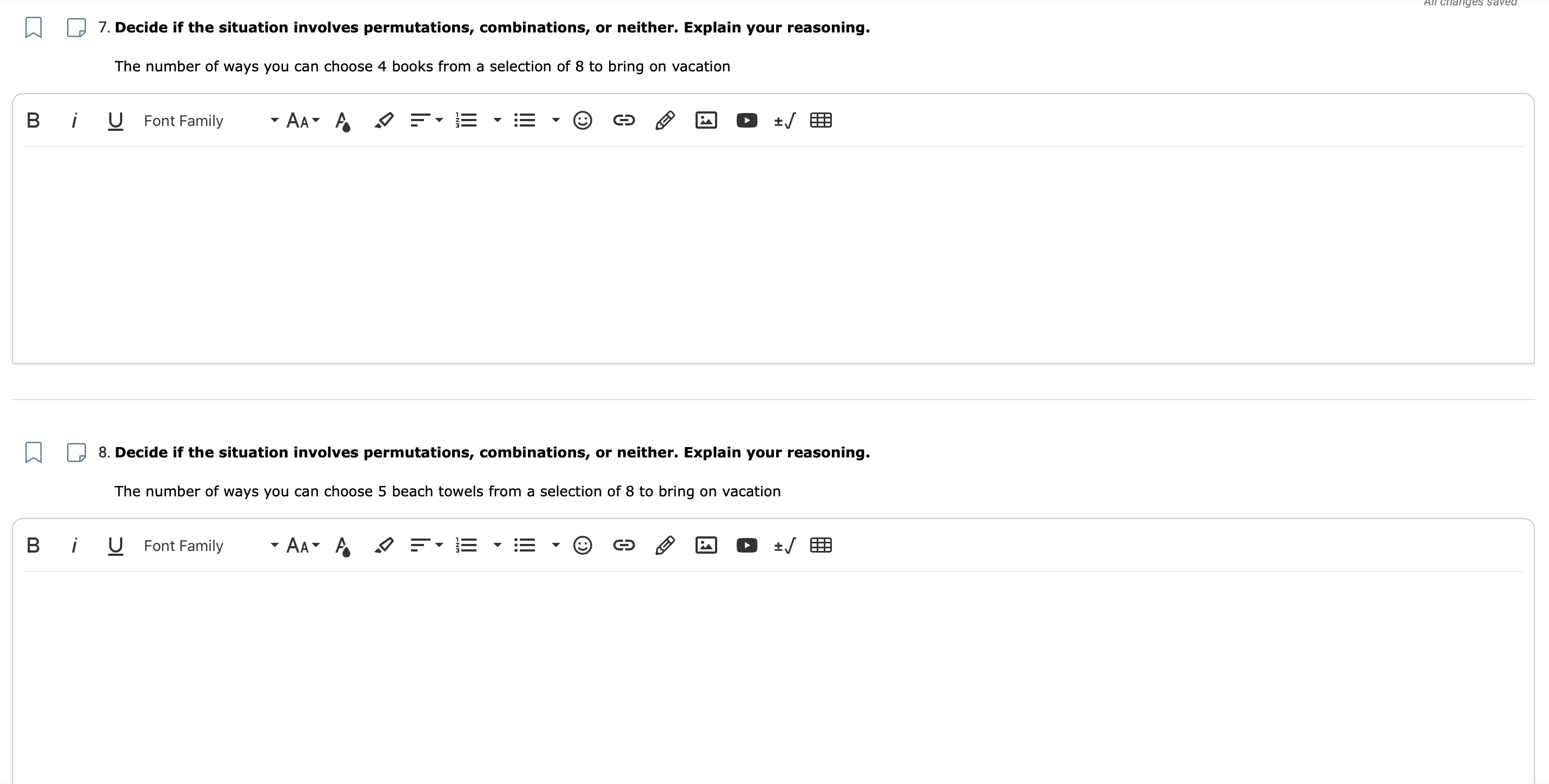
7. Decide if the situation involves permutations, combinations, or neither. Explain reasoning.

The number of ways you can choose 4 books from a selection of 8 to bring on vacation

8. Decide if the situation involves permutations, combinations, or neither. Explain reasoning.

The number of ways you can choose 5 beach towels from a selection of 8 to bring on vacation

9. Perform the indicated calculation.

6^P4

a) 2

b) 30

c) 360

d) 24

Permutations and Combinations Permutations Permutation - an ordered arrangement of objects. The number of different permutations of n distinct objects is n! n factorial - n! = n(n-1)(n-2)(n-3)...(2)(1) Practice 1 Find 3! Answer: 3! = (3) ( 2 ) ( 1 ) = 6 Practice finding factorial using the n! key on your calculator.Practice 8 The manager of an accounting department wants to form a three-person committee from the 20 employees in the department. In how many ways can a manager form this committee? Answer: This is a combination problem because a committee of 3 people is the same no matter how you order the people. C 20! 20! _20-19-18-17! _20-19-18 _ = _ _ =ll40 " r (203)!(3!) (17!)(3!) (l7!)(3!) (3-2-1) Practice using technology to find permutations and combinations. 3 nPr 2 201/((20-3) ! (3!) 6 1140 20 nor 3 1140 Examples and content taken from Elementary Statistics, Picturing the World, 7th edition, PearsonPractice 2 A collegiate athletic conference has 10 schools. How many different final standings are possible for the athletic conference football teams? Answer: 10! = (10)(9)(8)(7)(6)(5)(4)(3)(2)(1) = 3,628,800 Permutations of n 0mm Many times there is a need to choose groups of objects from a collection and put them in order. This would be called a permutation of n objects taken r at a time. The order matters in permutations. Practice 3 How many different permutations are there of the letters D, E, F grouped 2 at a time? List each one. Answer: DE, DF, EF, ED, FD, FE There are 6 different permutations. NOTE: DE is not the same as ED in permutations. This is considered a different arrangement. The order matters in each pair of letters. The formula for finding the number of permutations of n distinct objects taken rat a time is: P: n r (rtr)! where r S n Practice 4 How many different permutations are there of the letters A, B, C grouped 2 at a time. Answer: P 3! =(3)