complete exercises 18.1, 18.2 & 18.3 in 1 .java file (I will be using eclipse)

Listing 18.2 below

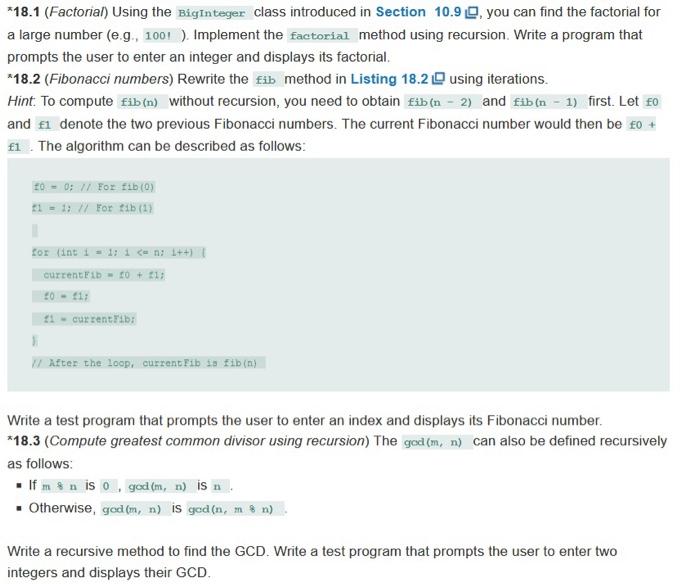
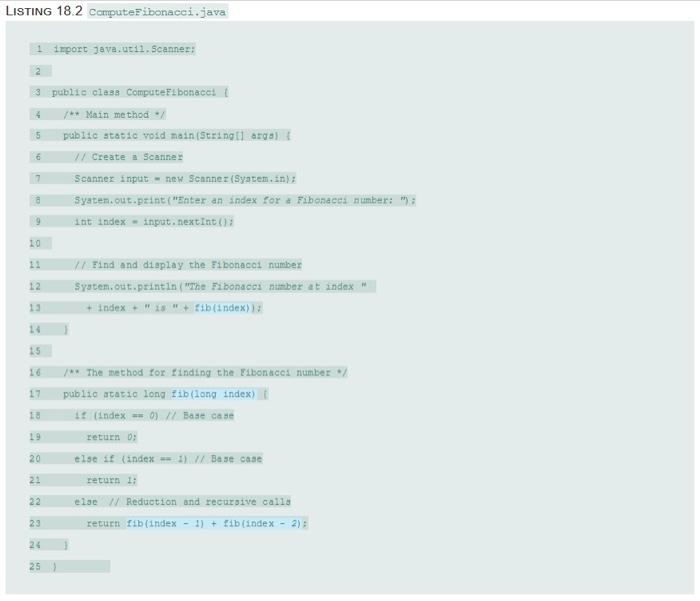
*18.1 (Factorial) Using the BigInteger class introduced in Section 10.9. you can find the factorial for a large number (.9., 1001 ). Implement the factorial method using recursion. Write a program that prompts the user to enter an integer and displays its factorial. *18.2 (Fibonacci numbers) Rewrite the fib method in Listing 18.2 using iterations. Hint. To compute Eib (n) without recursion, you need to obtain fib(n - 2) and fib(n - 1) first. Let to and el denote the two previous Fibonacci numbers. The current Fibonacci number would then be to + f1 The algorithm can be described as follows: + 10 = 0; // For 11b (0) 11 = 1// For tib (1) for (int i = 1: 1 em 1++) current i = 0 + 13 20 - 11 21 - currentrib: After the loop. current fib Eib (m) Write a test program that prompts the user to enter an index and displays its Fibonacci number. *18.3 (Compute greatest common divisor using recursion) The god (m, n) can also be defined recursively as follows: If m&n is o god (m, n) is n. . Otherwise, god (m, n) is god (n, men) Write a recursive method to find the GCD. Write a test program that prompts the user to enter two integers and displays their GCD. LISTING 18.2 Computer ibonacci.java 1 import java.util.Scanner: 4 5 3 public class Computer bonace /** Main method public static void main(String] args) 1/ Create a Scanner Scanner input-new Scanner(Syacem.in; syatem.out.print("Enter an index for a Fibonacua number: ant Index - input.nextInt (); 6 7 a 9 10 12 12 2/ Find and display the Fibonacci number System.out.println("the Fibonades amber at index + index + 1"+1b/index) 14 15 16 17 /* The method for finding the lonaco number public static long Iib (long index) 1+ index) // Base case 19 return 0; 20 else if (index = 1 Base case 21 return I: 22 else Reduction and recursive calls 23 return fib(index - 1) + fb (index - 2) 24 25