Complete the C program that makes many operations on 3D vector spaces by considering the following details.

The program contains a structure which represents a 3D vector, the main function and many functions prototypes. You must write the functions whose prototypes have been given.

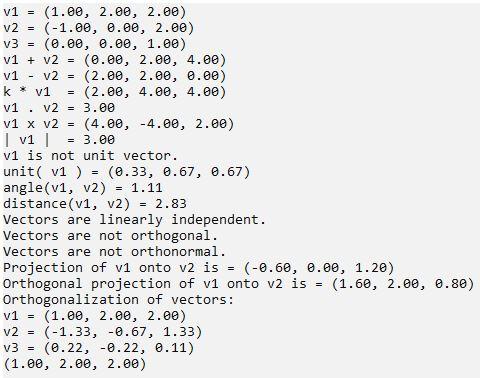
A sample output is given below for the given main function:

THE DEFINITION OF FUNCTIONS

void print_vector(const Vector v): 
It prints the vector as shown in output

Vector sum(const Vector v1, const Vector v2):
 It returns the sum of two vectors.

Vector diff(const Vector v1, const Vector v2): 
It returns the difference of two vectors.

double dot_product(const Vector v1, const Vector v2):
It returns the dot product of two vectors.

Vector cross_product(const Vector v1, const Vector v2):
It returns the cross product of two vectors.
 

double norm(const Vector v):
It returns the norm (length) of a vector.

int is_unitvector(const Vector v):
It check whether a vector is unit vector or not.

Vector unit(const Vector v):
It returns the unit vector of a vector.

Vector multiplyby_scalar(const Vector v1, const double c):
It returns the vector that is  the scalar multiplication of a vector by a constant.

double angle(const Vector v1, const Vector v2):
It returns the angle between two vectors.

double distance(const Vector v1, const Vector v2):
It returns the distance between two vectors. (|v1-v2|)

int are_linearly_independent(const Vector v1, const Vector v2, const Vector v3):
It check whether three vectors are linearly independent or not.

int are_orthogonal(const Vector v1, const Vector v2, const Vector v3):
It check whether three vectors are orthogonal or not.

int are_orthonormal(const Vector v1, const Vector v2, const Vector v3):
It check whether three vectors are orthonormal or not.

Vector projection(const Vector v1, const Vector v2):
It returns the projection vector of v1 onto the vector v2.

Vector orthogonal_projection(const Vector v1, const Vector v2):
It returns the orthogonal projection vector of v1 onto the vector v2.

int convert_2_orthogonal_basis(Vector *v1, Vector *v2, Vector *v3):
It converts three linearly independent vectors into an orthogonal basis by using the
Gram Schmidt Process. If vectors are not linearly independent, the function return 0,
otherwise it returns 1.

char* vector2str(const Vector v):
It converts a vector into a string (such as “(2.00, 1.00, 0.00)”) and it returns the string.
Clue: You can use sprint() function.

v1 = (1.00, 2.00, 2.00) (-1.00, 0.00, 2.00) v3 = (0.00, 0.00, 1.00) v2 v1 + V2 = v2 = = - v1 k * v1 v1 v2 = 3.00 v1 x v2 - (4.00, -4.00, 2.00) = 3.00 I v1 | v1 is not unit vector. I (0.00, 2.00, 4.00) (2.00, 2.00, 0.00) (2.00, 4.00, 4.00) = unit ( v1 ) = angle (v1, v2) (0.33, 0.67, 0.67) 1.11 = distance (v1, v2) = 2.83 Vectors are linearly independent. Vectors are not orthogonal. Vectors are not orthonormal. Projection of v1 onto v2 is = (-0.60, 0.00, 1.20) Orthogonal projection of v1 onto v2 is = (1.60, 2.00, 0.80) Orthogonalization of vectors: v1 = (1.00, 2.00, 2.00) v2 = (-1.33, -0.67, 1.33) v3 = (0.22, -0.22, 0.11) (1.00, 2.00, 2.00)