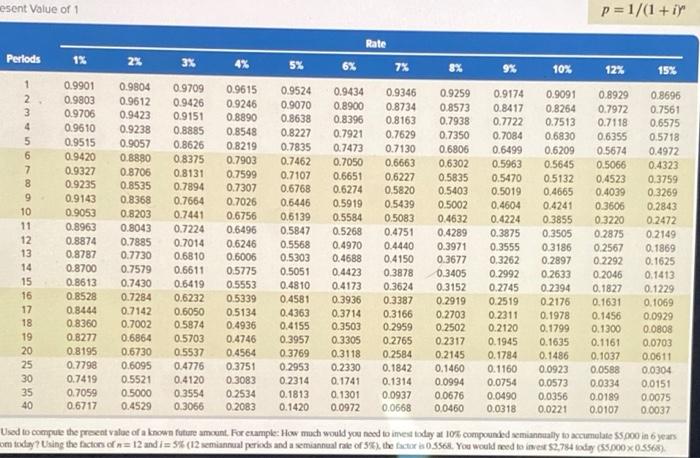
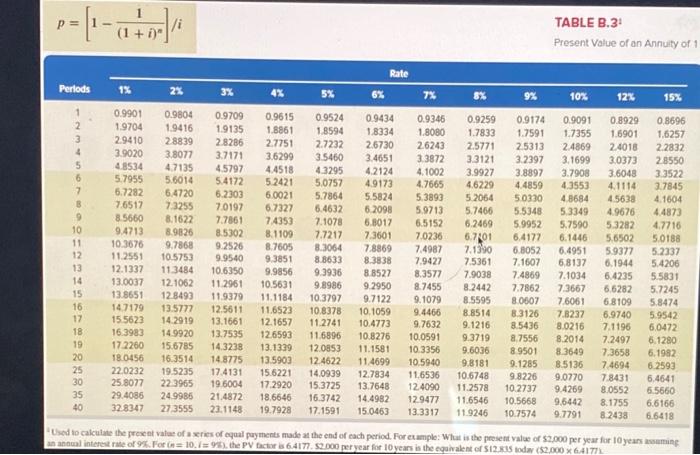
Compute the selling price of 10%, 10-year bonds with a par value of $320,000 and semiannual interest payments. The annual market rate for these bonds is 12%. Use present value Table B1 and Table B.3 in Appendix B. (Round all table values to 4 decimal places, and use the rounded table values in calculations.) Table Value Present Value Cash Flow $320,000 par (maturity) value 516,000 interest payment Price of Bond esent Value of 1 p=1/(1 + ir Rate Periods 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 12% 15% 1 0.9259 0.9174 0.9091 2 3 0.9804 0.9612 0.9423 0.8417 0.7722 0.8264 0.7513 0.8696 0.7561 0.6575 4 0.9238 0.6830 0.5718 5 0.9057 0.9901 0.9803 0.9706 0.9610 0.9515 0.9420 0.9327 0.9235 0.9143 0.9053 0.4972 6 0.7084 0.6499 0.5963 0.8880 0.9615 0.9246 0.8890 0.8548 0.8219 0.7903 0.7599 0.7307 0.7026 0.6756 0.6496 0.9434 0.8900 0.8396 0.7921 0.7473 0.7050 0.6651 0.6274 0.5919 0.5584 0.5268 0.9709 0.9426 0.9151 0.8885 0.8626 08375 0.8131 0.7894 0.7664 0.7441 0.7224 0.7014 0.6810 0.9346 0.8734 0.8163 0.7629 0.7130 0.6663 0.6227 0.5820 0.5439 0.5083 0.4323 7 8 0.9524 0.9070 0.8638 0.8227 0.7835 0.7462 0.7107 0.6768 0.6446 0.5139 0.5847 0.5568 0.5303 0.5051 0.4810 0.8706 0.8535 0.8368 0.8573 0.7938 0.7350 0.6806 0.6302 0.5835 0.5403 0.5002 0.4632 0.4289 0.3971 0.3677 0.3405 0.3152 0.5470 0.5019 0.4604 0.3759 0.3269 0.2843 9 10 0.8203 0.2472 11 0.8963 0.8043 0.4751 12 13 0.8874 0.8787 0.8700 0.7885 0.7730 0.7579 0.4224 0.3875 0.3555 0.3262 0.2992 0.2745 0.2519 0.4970 0.4688 0.4423 0.4173 14 0.6209 0.5645 0.5132 0.4665 0.4241 0.3855 0.3505 0.3186 0.2897 0.2633 0.2394 0.2176 0.1978 0.1799 0.1635 0.1486 0.8929 0.7972 0.7118 0.6355 0.5674 0.5066 0.4523 0.4039 0.3606 0.3220 0.2875 0.2567 0.2292 0.2046 0.1827 0.1631 0.1456 0.1300 0.1161 0.1037 0.0588 0.0334 0.0189 0.0107 0.6611 0.6246 0.6006 0.5775 0.5553 0.5339 0.5134 0.4936 0.2149 0.1869 0.1625 0.1413 0.1229 0.1069 0.7430 15 16 0.8613 0.8528 0.8444 0.8360 0.4581 0.6419 0.6232 0.6050 0.5874 0.5703 0.5537 0.4776 0.4440 0.4150 0.3878 0.3624 0.3387 0.3166 0.2959 0.2765 0.2584 0.1842 0.1314 0.0937 0.0668 0.2919 0.2703 0.2502 0.7284 0.7142 0.7002 0.6864 0.6730 0.6095 0.5521 0.2311 0.2120 0.1945 0.8277 0.4746 0.4363 0.4155 0.3957 0.3769 0.2953 0.2314 0.2317 0.0929 0.0808 0.0703 0.0611 19 20 25 30 35 40 0.8195 0.3936 0.3714 0.3503 0.3305 0.3118 0.2330 0.1741 0.1301 0.0972 0.7798 0.2145 0.1460 0.1784 0.1160 0.0754 0.0923 0.4564 0.3751 0.3083 0.2534 0.2083 0.7419 0.7059 0.6717 0.4120 0.3554 0.3066 0.5000 0.4529 0.1813 0.1420 0.0994 0.0676 0.0460 0.0304 0.0151 0.0075 0.0037 0.0573 0.0356 0.0221 0.0490 0.0318 Used to compute the present value of a known future amount. For example: How much would you need to invest today at 10% compounded semiannually to accumulate 5.000 in 6 years om today? Using the factors on=12 and i= 5% (12 semiannual periods and a semiannual rate of the actor : 0.556l. You would need to invest 2.784 today (55.000X05565) TABLE B.3: (1 + i)" 1/ Present Value of an Annuity of 1 Rate Periods 1% 2% 3% 4% 5% % 6% 7% 8% 9% 10% 12% 15% 1 0.8929 2 3 0.9091 1.7355 4 5 6 7 0.9709 1.9135 28286 3.7171 4.5797 5.4172 6.2303 7.0197 7.7861 8.5302 9.2526 9.9540 10.6350 2.4869 3.1699 3.7908 4.3553 4.8684 5.3349 5.7590 6.1446 B 9 10 0.9901 1.9704 29410 3.9020 48534 5.7955 6.7282 7.6517 8.5660 9.4713 10.3676 11.2551 12.1337 13.0037 13.8651 147179 15 5623 16.3983 172260 18.0456 22.0232 25.8077 29.4086 32.8347 0.9615 1.8861 2.7751 3.6299 4.4518 5.2421 6.0021 6.7327 7.4353 8.1109 8.7605 9.3851 9.9856 10.5631 11.1184 11.6523 12.1657 12.6593 13.1339 13.5903 0.9804 19416 28839 3.8077 4.7135 5,6014 6.4720 7.3255 8.1622 8.9826 9.7868 10.5753 113484 12.1062 128493 13.5777 14.2919 14.9920 15.6785 16.3514 19.5235 223965 24 9985 273555 11 0.9346 1.8080 26243 3.3872 4.1002 4.7665 5.3893 5.9713 6.5152 7.0236 7.4987 7.9427 12 13 14 15 16 17 0.9524 1.8594 2.7232 3.5460 4.3295 5.0757 5.7864 6.4632 7.1078 7.7217 8.3064 8.8633 9.3936 9.8986 10.3797 10.8378 11.2741 11.6896 12.0853 12.4622 14.0939 15.3725 16.3742 17.1591 0.9434 1.8334 2.6730 3.4651 4.2124 49173 5.5824 6.2098 6.8017 7.3601 7.8869 8.3838 8.8527 9.2950 9.7122 10.1059 10.4773 10.8276 11.1581 11.4699 12.7834 13.7648 14.4982 15.0463 0.9259 1.7833 2.5771 3.3121 3.9927 4.6229 5.2064 5.7466 6.2469 6.7101 7.1390 7.5361 7.9038 8.2442 8.5595 8.8514 9.1216 9.3719 9.6036 9.8181 10.6748 11.2578 11.6546 11.9246 0.9174 1.7591 25313 3.2397 3.8897 4.4859 50330 5.5348 5.9952 6.4177 6.8052 7.1607 7.4869 7.7862 8.0507 8.3126 8.5436 8.7556 8.9501 9.1285 9.8226 10.2737 10.5668 10.7574 8.3577 0.8696 1.6257 22832 28550 3.3522 3.7845 4.1604 4.4873 4.7716 5.0188 5.2337 5.4206 5.5831 5.7245 5.8474 5.9542 6,0472 6.1280 6.1982 6.2593 6.4641 6.5660 6.6166 6.6418 1.6901 24018 3.0373 3.6048 4.1114 4.5638 4.9676 5.3282 5.6502 59377 6.1944 6.4235 6,6282 6.8109 6.9740 7.1196 7.2497 7.3658 74694 7.8431 8.0552 8.1755 8.2438 11.2961 11.9379 18 6.4951 6,8137 7.1034 7.3667 7.6061 7.8237 8.0216 8.2014 8.3649 8.5136 9.0770 9.4269 9.6442 9.7791 19 8.7455 9.1079 9.4466 9.7632 10.0591 10.3356 10.5940 11.6536 124090 12 9477 13.3317 12.5611 13.1661 13.7535 14.3238 14.8775 17.4131 19.6004 21.4872 23.1148 20 25 30 35 40 15.6221 17.2920 18,6646 19.7928 Used to calculate the present value of nies of equal payments made at the end of each period. For example: What is the present value of $2.000 per year for 10 years aming an anal interest rate Foto 10.1 the Pictor 6,4177.52.000 per year for 10 years in the equivalent 12.35 toda ($2,000 X 6417