Computer Science Python problem about numerical computing.

Code runs on jupyter notebook with python3 kernel.

It has a long background code, but real question shouldn't be long.

I will give thumb up, thank you!

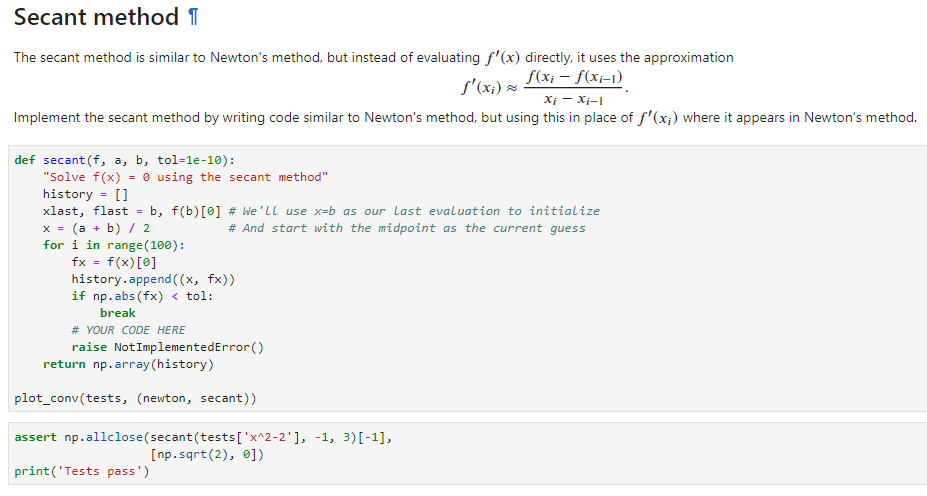
background:

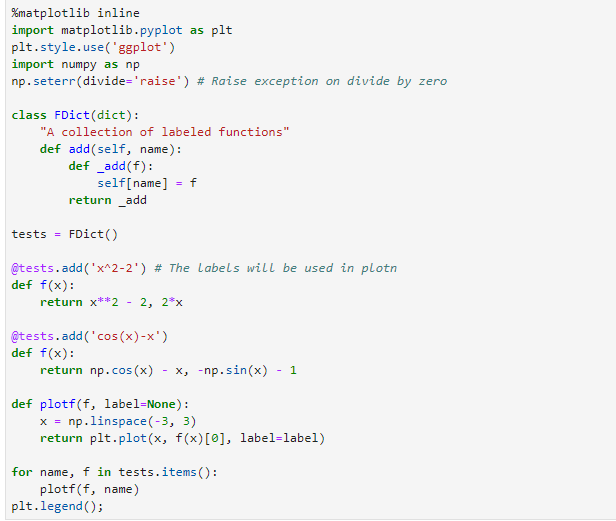
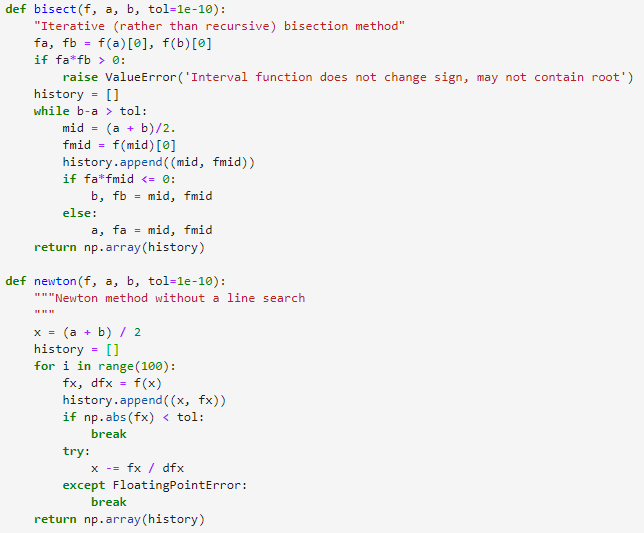
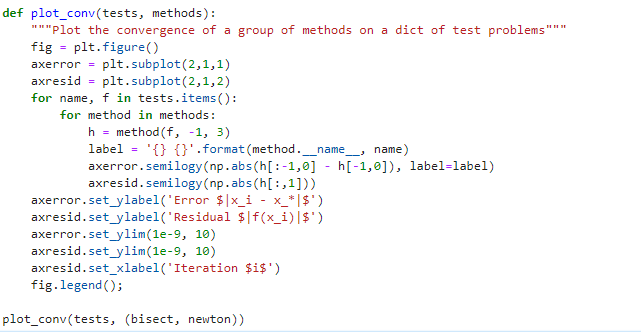
Question:

Test case:

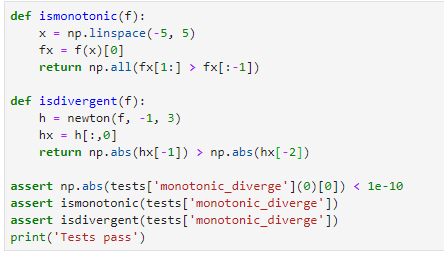
I will be appreciate if you can also look at this question. but not require, thank you!

%matplotlib inline import matplotlib.pyplot as plt plt.style.use 'ggplot') import numpy as np np.seterr(divide-' raise') # Raise exception on divide by zero class FDict (dict): "A collection of labeled functions" def add(self, name): def _add(f): self[name] f return add tests FDict() @tests.add("X"2-2') # The Labels will be used in plotn def f(x): return x *2 -2, 2*x @tests.add'cos(x)-x') def f(x): return np. cos (x) -x, -np. sin(x) -1 def plotf(f, label-None): xnp.linspace(-3, 3) return plt.plot(x, f(x)[0], label-label) for name, f in tests.items (): plotf(f, name) plt.legend) def bisect(f, a, b, tol-1e-10): "Iterative (rather than recursive) bisection method fa, fb f(a)[e], f(b)[o] if fa fb >0: raise ValueError( 'Interval function does not change sign, may not contain root') history -[l while b-a >tol: mid - (a b)/2 fmid f(mid)[0] history.append((mid, fmid)) b, fb-mid, fmid else: a, fa- mid, fmid return np.array(history) def newton(f, a, b, tol-1e-10): " " Newton method without a line search x-(a b)/ 2 history- for i in range (100): fx, dfx -f(x) history.append((x, fx)) if np.abs(fx) 0 for all x. . @tests.add( monotonic_diverge) def f(x): Strictly monotonically increasing function with a simple root at x-0 for which Newton's method diverges with initial guess x-1. Remember that the interface requires that this function and its derivative be defined. # YOUR CODE HERE raise NotImplementedError) plott(testsmonotonic-diverge' ] ) ; def smonotonic(f): x n.inspace(-5, 5) fx f(x)[0] return np.all (fx[1:] > fx[:-1]) def isdivergent(f): h - newton(f, -1, 3) return np.abs (hx[-]np.abs(hx[-2]) assert np.abs (tests[ monotonic_diverge'1(0) [e])1e-10 assert ismonotonic(tests[ monotonic_diverge']) assert isdivergent(tests['monotonic_diverge'1) print('Tests pass) Secant method T The secant method is similar to Newton's method, but instead of evaluating f'(x) directly, it uses the approximation Xi Xi- Implement the secant method by writing code similar to Newton's method, but using this in place of f'(xi) where it appears in Newton's method. def secant(f, a, b, tol-1e-10): "Solve f(x) using the secant method" history -[l xlast, flast b, f(b)[0] # We'll use x-b as our last evaluation to initialize x=(a + b) / 2 for i in range(100): # And start with the midpoint as the current guess fx f(x)[0] history.append((x, fx)) if np.abs(fx)