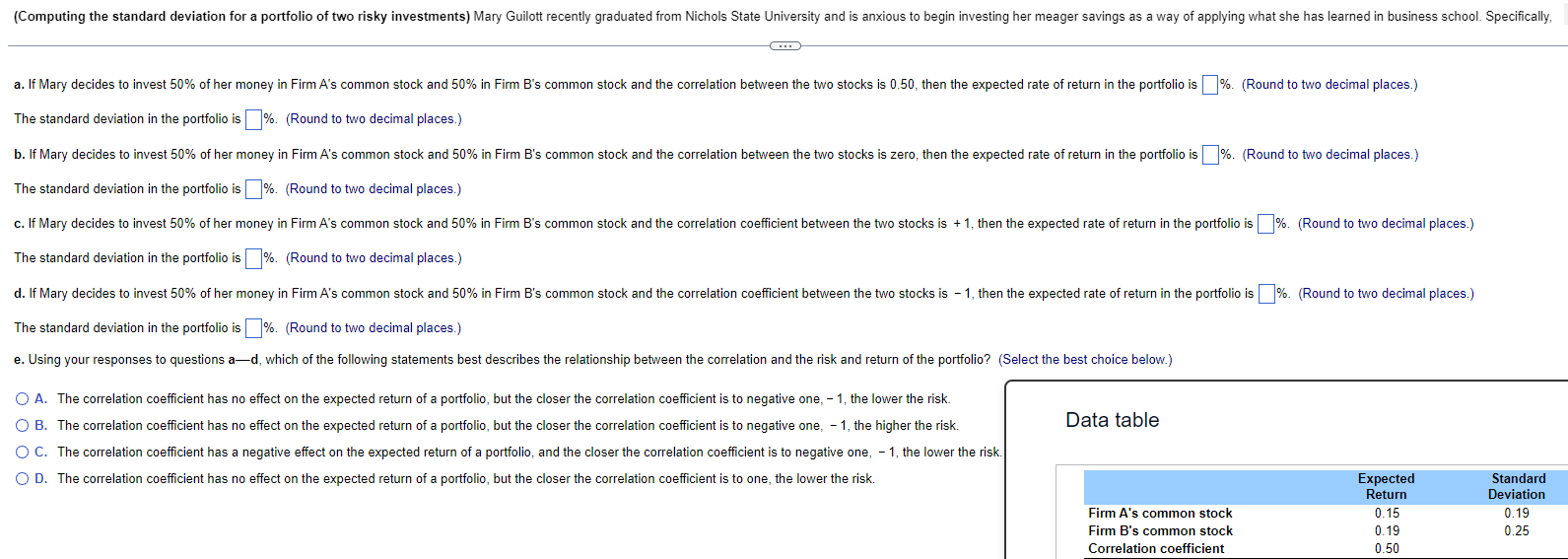
(Computing the standard deviation for a portfolio of two risky investments) Mary Guilott recently graduated from Nichols State University and is anxious to begin investing her meager savings as a way of applying what she has learned in business school. Specifically, a. If Mary decides to invest 50% of her money in Firm A's common stock and 50% in Firm B's common stock and the correlation between the two stocks is 0.50, then the expected rate of return in the portfolio is %. (Round to two decimal places.) The standard deviation in the portfolio is %. (Round to two decimal places.) b. If Mary decides to invest 50% of her money in Firm A's common stock and 50% in Firm B's common stock and the correlation between the two stocks is zero, then the expected rate of return in the portfolio is %. (Round to two decimal places.) The standard deviation in the portfolio is %. (Round to two decimal places.) c. If Mary decides to invest 50% of her money in Firm A's common stock and 50% in Firm B's common stock and the correlation coefficient between the two stocks is + 1, then the expected rate of return in the portfolio is %. (Round to two decimal places.) The standard deviation in the portfolio is %. (Round to two decimal places.) d. If Mary decides to invest 50% of her money in Firm A's common stock and 50% in Firm B's common stock and the correlation coefficient between the two stocks is -1, then the expected rate of return in the portfolio is %. (Round to two decimal places.) The standard deviation in the portfolio is %. (Round to two decimal places.) e. Using your responses to questions ad, which of the following statements best describes the relationship between the correlation and the risk and return of the portfolio? (Select the best choice below.) A. The correlation coefficient has no effect on the expected return of a portfolio, but the closer the correlation coefficient is to negative one, -1, the lower the risk. B. The correlation coefficient has no effect on the expected return of a portfolio, but the closer the correlation coefficient is to negative one, -1, the higher the risk. C. The correlation coefficient has a negative effect on the expected return of a portfolio, and the closer the correlation coefficient is to negative one, -1, the lower the risk. OD. The correlation coefficient has no effect on the expected return of a portfolio, but the closer the correlation coefficient is to one, the lower the risk. Data table Expected Return Standard Deviation Firm A's common stock 0.15 0.19 Firm B's common stock Correlation coefficient 0.19 0.25 0.50