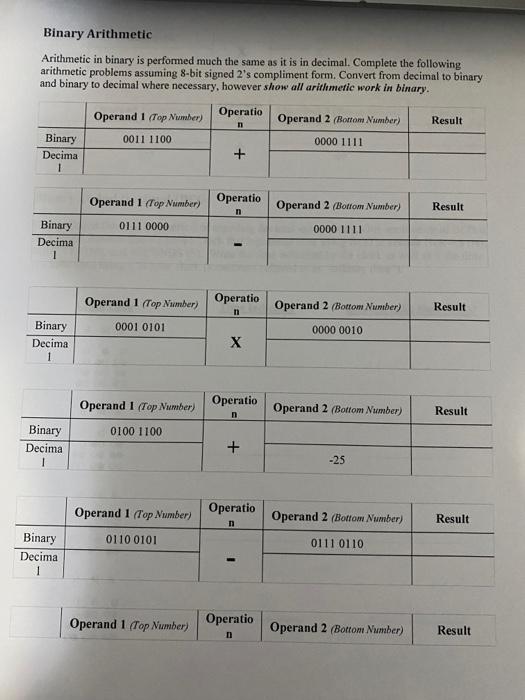
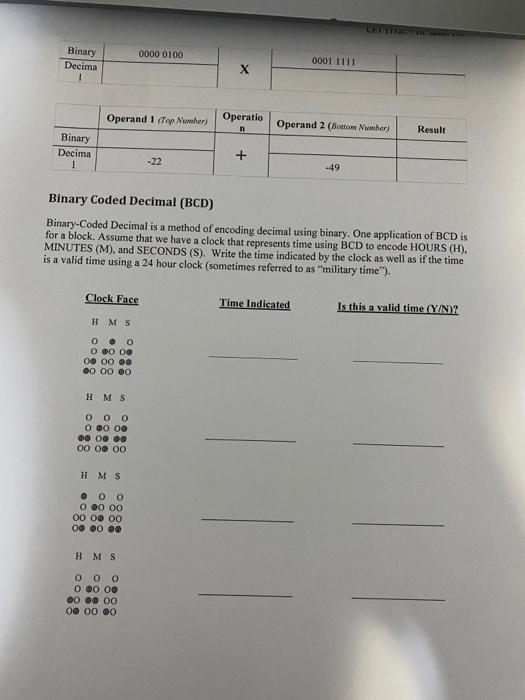
CONCEPT Much of digital design requires a good understanding of the binary number systems. Because having solid foundation in the binary number system will make the rest of the course much easier, we will spend the first lab reinforcing the principles of binary number systems. Counting in Different Bases Binary is a numerical system that uses a base of radix-2. While we are more accustomed to using a radix of 10 , counting works exactly the same with different bases. Complete the following chart by counting to decimal 15 in each of the different bases. Converting Between Binary, Decimal, and Hexadecimal It is important to be able to convert between different bases. Fill in the following table by converting the known value to the two unknown bases. Representing Negative Numbers in Binary To represent negative numbers in binary we must sacrifice one of the bits to indicate sign (positiveegative). We have three ways of doing this; Sign-Magnitude, I's Compliment, and 2's Compliment. Assuming 1-Byte (8-bit) values fill in the missing blanks in the following table: Binary Arithmetic Arithmetic in binary is performed much the same as it is in decimal. Complete the following arithmetic problems assuming 8-bit signed 2's compliment form. Convert from decimal to binary and binary to decimal where necessary, however show all arithmetic work in binary. Binary Coded Decimal (BCD) Binary-Coded Decimal is a method of encoding decimal using binary. One application of BCD is for a block. Assume that we have a clock that represents time using BCD to encode HOURS (H), MINUTES (M), and SECONDS (S). Write the time indicated by the clock as well as if the time is a valid time using a 24 hour clock (sometimes referred to as "military time"). H M S 000 O 0000 O OO OO OO OO OO Binary Crossword Challenge This puzzle consists completely of binary numbers, so all the characters needed to fill in the squares will be 0 s or 15 . The crossword is a 44 square grid, so all numbers will be written in binary, with 4 digits; e.g., 1 will be 0001,2 will be 0010 , and 4,0100 . The NOT operation changes all 0 s to 1's and all 15 to 0 s; e.g., NOT(0110) is 1001 and NOT (1010) is 0101. Rows (Across): Columns (Down): 1. "2 Down" 2 1. NOT " 2 Across" 2. A triangular number * 2. NOT "1 Across" 3. The cube of ("4 Down" - 2) 3. "2 Across" 2 4. "3 Across" + "3 Down" 4. "4 Across" - "1 Across" * HINT: A triangular number is the number of dots in an equilateral triangle uniformly filed with dots. For example, three dots can be arranged in a triangle; thus three is a triangle number