Answered step by step

Verified Expert Solution

Link Copied!

Question

1 Approved Answer

Posted on Jan 11, 2023

Conclude whether the following series is conditionally convergent, absolutely convergent, or diverges. Provide justification. n=2 n cos (1) In(n)(n+7)4

Conclude whether the following series is conditionally convergent, absolutely convergent, or diverges. Provide justification.

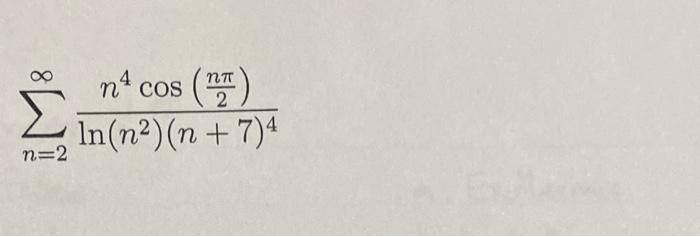
$\sum_{n=2}^{\infty} \frac{n^{4} \cos \left(\frac{n \pi}{2}ight)}{\ln \left(n^{2}ight)(n+7)^{4}}$

n=2 n cos (1) In(n)(n+7)4

Step by Step Solution

★★★★★

3.40 Rating (156 Votes )

There are 3 Steps involved in it

Step: 1

nt cos 112 en n n7 Now Here n is always a positive so 03 111 0 SW ... blur-text-image

Get Instant Access to Expert-Tailored Solutions

See step-by-step solutions with expert insights and AI powered tools for academic success

Step: 2

Step: 3

Ace Your Homework with AI

Get the answers you need in no time with our AI-driven, step-by-step assistance

Get Started

Recommended Textbook for

Calculus Early Transcendentals

Authors: James Stewart

7th edition

538497904, 978-0538497909

More Books

Students also viewed these Accounting questions

Question

★★★★★

Determine whether the series is absolutely convergent or conditionally convergent. (-1)*-1 00 In 1

Answered: 1 week ago

Question

★★★★★

Determine whether the series is absolutely convergent or conditionally convergent.

Answered: 1 week ago

Question

★★★★★

Determine whether the series is absolutely convergent or conditionally convergent.

Answered: 1 week ago

Question

★★★★★

Match the accounting terminology to the definitions. 1. Sarbanes-Oxley Act 2. Internal control 3. Encryption 4. Separation of duties 5. Internal auditors

Answered: 1 week ago

Question

★★★★★

Apple Inc. designs, manufactures, and markets personal computers and related personal computing and communicating solutions for sale primarily to education, creative, consumer, and business...

Answered: 1 week ago

Question

★★★★★

(a) How much more output does the $18 trillion U.S. economy produce when GDP increases by 1.0 percent? (b) By how much does this increase the average (per capita) income if the population is 320...

Answered: 1 week ago

Question

★★★★★

Irene has a Facebook page and she is very keen to have a large number of friends there. The number of friends added to her page follows a Poisson process with a rate of ???? = 3 persons per week. (i)...

Answered: 1 week ago

Question

★★★★★

Classify the following decisions as being characteristic of strategic planning, tactical planning, managerial control, or operational control. Determining the mix of products to manufacture this year...

Answered: 1 week ago

Question

★★★★★

AuctionCo.com sells used products collected from different suppliers. Assume a customer ordered a used bicycle through AuctionCo.com for $30. The cost of this bicycle is $20 to AuctionCo.com. The...

Answered: 1 week ago

Question

★★★★★

A partial adjusted trial balance of Manumaleuna Company at January 31, 2012, shows the following. InstructionsAnswer the following questions, assuming the year begins January 1.(a) If the amount in...

Answered: 1 week ago

Question

★★★★★

A sleeper cab adds how much to the cost of a tractor?

Answered: 1 week ago

Question

★★★★★

What should Disney do to mitigate the losses stemming from the two scandals and to minimize the likelihood of such reputation-threatening incidents recurring in the future?

Answered: 1 week ago

Question

★★★★★

Calculate the productivity for the following operations: a.Three employees process 600 insurance policies in a week. They work 8 hours per day, 5 days per week.

Answered: 1 week ago

Question

★★★★★

Is there any lesson of significance that you have learned from the Goal? If so, explain the relevance of this operational phenomenon to service-based and manufacturing organizations.

Answered: 1 week ago

Question

★★★★★

The OM supervisor informs you, the researcher, that the data has a large standard deviation. What data pattern would you expect to observe once you generated a time series trend?

Answered: 1 week ago

Question

★★★★★

Kari, a member of the Wave Earbuds research team, will be presenting findings about the prototype for the new wireless earbuds during an upcoming meeting. Since this meeting will have representatives...

Answered: 1 week ago

Question

★★★★★

CALCULATOR FULL SCREEN RINTER VERSION Teal Mountain Inc. is trying to determine the value of its ending inventory as of February 28, 2017, the company's year end. The accountant counted everything...

Answered: 1 week ago

Question

★★★★★

Use the T account for Cash below to record the portion of each of the following transactions, if any that affect cash. How do these transactions affect the companys liquidity? Jan. 2 Provided...

Answered: 1 week ago

Question

★★★★★

Graph the curve and visually estimate its length. Then use your calculator to find the length correct to four decimal places. y = x2 + x3, 1 x 2

Answered: 1 week ago

Question

★★★★★

Given that find the limits that exist. If the limit does not exist, explain why. lim f(x) = 4 lim g(x)--2 lim h(x) =0 lim 5glx)] lim [g(x)] lim Vf(x) -2 3f(x) lim 2 ga) g(x) lim lim fx)

Answered: 1 week ago

Question

★★★★★

A direction field for the differential equation is y' = x cos y is shown.

Answered: 1 week ago

Question

★★★★★

Families USA, a monthly magazine that discusses issues related to health and health costs, surveyed 20 of its subscribers. It found that the annual health insurance premiums for a family with...

Answered: 1 week ago

Question

★★★★★

Ms. Maria Wilson is considering running for mayor of the town of Bear Gulch, Montana. Before completing the petitions, she decides to conduct a survey of voters in Bear Gulch. A sample of 400 voters...

Answered: 1 week ago

Question

★★★★★

The Fox TV network is considering replacing one of its prime-time crime investigation shows with a new family-oriented comedy show. Before a final decision is made, network executives commission a...

Answered: 1 week ago

Previous Question Next Question