Question
Confidence Intervals and Hypothesis Tests Comparing TWO Proportions, Differences or Means AND ANOVA (Analysis of Variance) This first part involves calculating: Confidence Interval for two
Confidence Intervals and Hypothesis Tests Comparing TWO Proportions, Differences or Means AND ANOVA (Analysis of Variance)
This first part involves calculating:
- Confidence Interval for two population Proportions
- Hypothesis Test for two population Proportions
- Hypothesis Test for two population Differences
- Confidence Interval for two population differences
- Hypothesis Test comparing two population Means
1) (made-up data)Confidence Interval Problem for Proportions: Calculate a 95% confidence interval for these proportions. SHOW YOUR "E" SETUP & CALCULATIONS. The same assumptions must be met to ensure the statistical analysis is valid and Make sure to calculate the proportions first.
High school students take the AP tests in different subject areas. This year 150 students took the biology exam of which 85 were female. And, 220 students took the calculus exam of which 100 were female. Calculate the difference in the PROPORTION of female students taking the biology exam versus female students taking the calculusexam using a 95% confidence level.
E = z-critical * sqrt[ (p-hat1 * q-hat1)1) + (p-hat2 * q-hat2)2)]
2) (made-up data)Hypothesis Test problem for Proportions: Assume a 1% significance level. The same assumptions must be met to ensure the statistical analysis is valid and calculate the proportions first.
SHOW Z-Test SETUP AND Z-Critical value the z-Test was compared to. Also, use software to calculate the p-Value. Do both support the same conclusion? (they MUST). State your real-world conclusion?
Are more children diagnosed with Autism Spectrum Disorder in States that have urban areas over States that are mostly rural? In an urban State, there were are 300 3rd grade students diagnosed with ASD out of 18,500 3rd graders tested. In a rural state, there were 55 3rd grade students diagnosed with ASD out of 2,300 3rd graders tested. Is there enough evidence to show that the proportion of children diagnosed with ASD in an urban State is more than the proportion in a rural State? Test at the ? = 1% level.
3) Coin-Toss Data- We had ____ sets of 30-flipped coin sets. Some used ONE coin and some 30 different coins. Conduct a hypothesis test on the proportion of HEADS using ONE coin versus the proportion of HEADS using 30 coins. Is there a significant difference (5% level)?
t-Test = [(x-bar1 - x-bar2) -(1 - 2)] / sqrt ( s121 + s222)
To find the t-Critical we need the degrees of freedom (df) and the formula to calculate df is "hairy". As presented earlier, the simpler formula that is used by some statisticians: df = (n1 - 1) + (n2 - 1)
4) (made-up data) Hypothesis Test problem for TWO population DIFFERENCES (not proportions or means) comparison hypothesis test (NOT a proportion problem - so we use t-values, not z-values). SHOW t-TEST SETUP and calculation, AND for the t-Critical, what SIGNIFICANCE LEVEL (the column) and what df (which row) were used and what the t-Critical value is.
Do people avoid driving on Friday the 13th? Here are data on 20 Fridays: 10 on the 13th and the other 10 on the Friday before. For the DIFFERENCES, Calculate the MEAN and SD between traffic on these two Fridays at the 95% level(alpha = 5%);
Traffic Count
| Dates | 6th (x1) | 13th (x2) | d = (x1 - x2) |
| 1990, July | 139246 | 138548 | |
| 1990, July | 138012 | 132908 | |
| 1991, September | 137055 | 136018 | |
| 1991, September | 140675 | 131843 | |
| 1991, December | 123552 | 121641 | |
| 1991, December | 121139 | 120723 | |
| 1992, March | 128293 | 125532 | |
| 1992, March | 124631 | 120249 | |
| 1992, November | 124609 | 125770 | |
| 1992, November | 119584 | 116263 |
For the differences (all d's) the MEAN = _______ and the SD = __________
TEST STATISTIC: t-Test = (d-bar -d)/sd /sqrt(n) = ____; The t-Critical with (n-1) df for? = 5% is______
What is the software-generated p-value for the t-Test? ______
What is your math conclusion and your real-world conclusion?
5) Confidence Interval problem for two population DIFFERENCES (not means or proportions) that have the SAME NUMBER OF DATA VALUES (n1 = n2).
Using the same traffic count data and statistics as above, the margin of error, E, the formula isE = t-critical * sd/sqrt(n)
We will assume a significance level of? = 5%(95% confidence level) with n=10 data points, hence df = (10 - 1 ) = 9, so t-critical =______ ?
What are the MEAN ______and SD _____for the "differences"?
E = _______ * _______ / ______ = __________ (fill in the different values and the calculated result) .
Our Confidence Intervalis (d-bar - E) d d
Real-world Conclusion: Whose median income mean is larger and by how much?
(IF this or any CI includes zero there is NO difference)
(5) (made-up data) Hypothesis Test problem comparing two population MEANS. Make sure to show your setup for the t-Test, df, and how you found the t-Critical.Also, use software to find the p-value (probability) is it larger or smaller than?? Does this conclusion match the one based on the t-Test versus t-Critical? (It must). For the p-value, make sure you know which area (right or left) you need to use (greater than or less than). (If NO Confidence Level or? is provided assume 95% and 5%, respectively)
Median Income for Males
| $42,951 | $52,379 | $42,544 | $37,488 | $49,281 | $50,987 | $60,705 |
| $50,411 | $66,760 | $40,951 | $43,902 | $45,494 | $41,528 | $50,746 |
| $45,183 | $43,624 | $43,993 | $41,612 | $46,313 | $43,944 | $56,708 |
| $60,264 | $50,053 | $50,580 | $40,202 | $43,146 | $41,635 | $42,182 |
| $41,803 | $53,033 | $60,568 | $41,037 | $50,388 | $41,950 | $44,660 |
Median Income for Females
| $31,862 | $40,550 | $36,048 | $30,752 | $41,817 | $40,236 | $47,476 |
| $60,332 | $33,823 | $35,438 | $37,242 | $31,238 | $39,150 | $34,023 |
| $33,269 | $32,684 | $31,844 | $34,599 | $48,748 | $46,185 | $36,931 |
| $29,548 | $33,865 | $31,067 | $33,424 | $35,484 | $41,021 | $47,155 |
| $42,113 | $33,459 | $32,462 | $35,746 | $31,274 | $36,027 | $37,089 |
t-Test = [(x-bar1 - x-bar2) -(1 - 2)] / sqrt ( s121 + s222)
To find the t-Critical we need the degrees of freedom (df) and the formula to calculate df is "hairy". As presented earlier, the simpler formula that is used by some statisticians: df = (n1 - 1) + (n2 - 1)
(If you want to copy the above Tables into Excel, highlight the entire Table, right-click and "COPY" than before you paste, highlight the same number of columns (7 here) across Excel, then hit "paste". If you only highlight one column it may not do anything or it may put all the data vertically in that column. )
6) AnotherHypothesis Test problem comparing two populations MEANS for the two-medication "time to take effect" example. Work it just as you did the prior problem (#5)
t-Test = [(x-bar1 - x-bar2) -(1 - 2)] / sqrt ( s121 + s222)
To find the t-Critical we need the degrees of freedom (df): df = (n1 - 1) + (n2 - 1)
Also, find the p-value
Bottom line: Is there a significant difference between the mean "time to take effect" for these two medications and if so, which medication is significantly faster.
MOVING ON TO ANOVA (Analysis of Variance)
We have just finished comparing the means of TWO data sets to determine if there is a significant difference between them. We have used the z-Test (proportions) and the t-Test to do this. We FINALLY find a use for the VARIANCE!
We haven't used the variance very much in this course, just its square root, the standard deviation.
There is a LOT of squaring (and maybe swearing) in ANOVA calculations and if you recall from your Week 1 exercise in calculating variance, we squared distances to make any negative ones, positive. This is what we are essentially doing here but in multiple dimensions.
We are basically comparing the Means and Variances of multiple populations (three or more) to see if ANY are significantly different from the others. (see the Additional Guidance attachment for assistance.) It will NOT tell us which population is different, however.
7) (made-up data) WORK THIS PROBLEM:
| Plant 1 | Plant 2 | Plant 3 | Plant 4 | Plant 5 |
| 1.2 | 16.4 | 12.1 | 11.5 | 24 |
| 10.1 | -6 | 9.7 | 10.2 | -3.7 |
| -2 | -11.6 | 7.4 | 3.8 | 8.2 |
| 1.5 | -1.3 | -2.1 | 8.3 | 9.2 |
| -3 | 4 | 10.1 | 6.6 | -9.3 |
| -0.7 | 17 | 4.7 | 10.2 | 8 |
| 3.2 | 3.8 | 4.6 | 8.8 | 15.8 |
| 2.7 | 4.3 | 3.9 | 2.7 | 22.3 |
| -3.2 | 10.4 | 3.6 | 5.1 | 3.1 |
| -1.7 | 4.2 | 9.6 | 11.2 | 16.8 |
| 2.4 | 8.5 | 9.8 | 5.9 | 11.3 |
| 0.3 | 6.3 | 6.5 | 13 | 12.3 |
| 3.5 | 9 | 5.7 | 6.8 | 16.9 |
| -0.8 | 7.1 | 5.1 | 14.5 | |
| 19.4 | 4.3 | 3.4 | 5.2 | |
| 2.8 | 19.7 | -0.8 | 7.3 | |
| 13 | 3 | -3.9 | 7.1 | |
| 42.7 | 7.6 | 0.9 | 3.4 | |
| 1.4 | 70.2 | 1.5 | 0.7 | |
| 3 | 8.5 | |||
| 2.4 | 6 | |||
| 1.3 | 2.9 |
What is the NULL Hypothesis, Ho:
What is the Alternate Hypothesis, Ha:
In the formula: "k" is simply the number of groups and capital "N" is the TOTAL of ALL the data values involved (all groups together) and small "n" is the AVERAGE number of data points per group = (N/k)
The 5 groups involved have DIFFERENT numbers of samples (n), but they are relatively close, so I used the AVERAGE "n" and got an F-Test close to the text value. This is NOT technically the official way to calculate F, but the official way is quite complex for an introductory overview)
| Plant 1 | Plant 2 | Plant 3 | Plant 4 | Plant 5 | |
| n | |||||
| Mean | |||||
| Variance |
- Fill in the Table above ^
- Determine k = _____
- Calculate N = ______
- Calculate the average n = ____
- Calculate the VARIANCE of the 5 sample means = ______ *average-n = _______ = _________
- Calculate the AVERAGEVARIANCE of the 5-groups' variances = _____________
F-Test = (e) / (f) = _________(This is by using the average n)
(The Text software gets an F-Test of 1.16)
To find the F-Critical value:
- Calculate the first degrees of freedom: df1 = k - 1 = ____
- Calculate the second degrees of freedom:df2 = N - k = ____
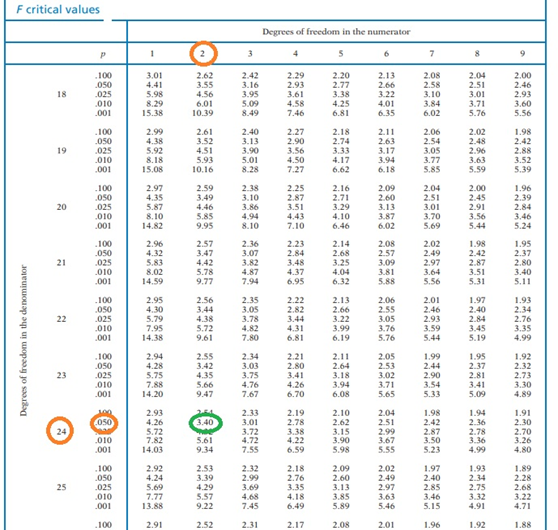
- Find the F-Critical from the F-Table below for these degrees of freedom (df) and? = 1% : ___________
- Compare your F-Test to the F-critical and do you accept or reject Ho?____________
You can use this website:https://stattrek.com/online-calculator/f-distribution.aspx to find the p-value (probability) for a given F-Test statistic. What is the p-value for the F-Test you calculated? ___________
Comparing these to the? = 0.01 or 1%, would you draw the same Reject/Fail to reject Ho conclusion?
8) COIN TOSS RESULTS: We had ____ sets of 30-flipped coin sets. Some used ONE coin and some 30 different coins. Is there a significant difference in those results, i.e., are any numbers of HEADS significantly different in the one-coin group or in the 30 coin group? Keep in mind that even IF there is a significant difference, we won't be able to tell which data set(s) is or are different. Here is a Table of those "HEADS" results (number out of 30 tosses) and the sampling protocol used (one coin or 30 coins)
Now, IF you want a video on how to REALLY work ANOVA for different sample sizes, check one of these (or both) out:
https://www.youtube.com/watch?v=0XsovsSnRuw
https://www.youtube.com/watch?v=q48uKU_KWas
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


