Consider a European call option on a non-dividend-paying stock; when the option is written, the stock price is S₀, the volatility of the stock price is , the strike price is K, the continuously compounded risk-free rate is r, and the term to expiration is T; let c be the price of the option. The Black-Scholes formula for the option price is

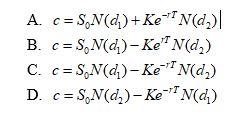
where N(x) is the cumulative probability distribution function for a standardized normal distribution and d₁ and d₂ are parameters dependant on the structure of the option, the level of interest rates, and the volatility of the stock price.

13. (a) Using the terminology of the last question (re-printed above Question 8 from the multiple choice section), specify the Black-Scholes formula for the price of a European put option on a non-dividend-paying stock

(b) Explicitly describe the relationship of the parameters d₁ and d₂ to the structure of the option, the level of interest rates and the volatility of the stock price and the relationship of the parameters to each other; use the notation of the last question (e.g., write the formulas for d₁ and d₂ )

(c) We found that for a dividend yielding stock that there was a simple enhancement possible to convert the result in question 3) to the case of a European call option on a dividend yielding stock. Let q represent the dividend yield and describe the enhancement (which we found appropriate in many representations). Also, show the result for the European call option on a dividend yielding stock (include the formula for d₁ and d₂ ).

A. c = SN(d)+ Ke-N(d.) B. c = SN(d)-Ken(d,) C. c=SN(d)-Ke-'T N(d)) D. c = SN(d)-Ke-N(d)