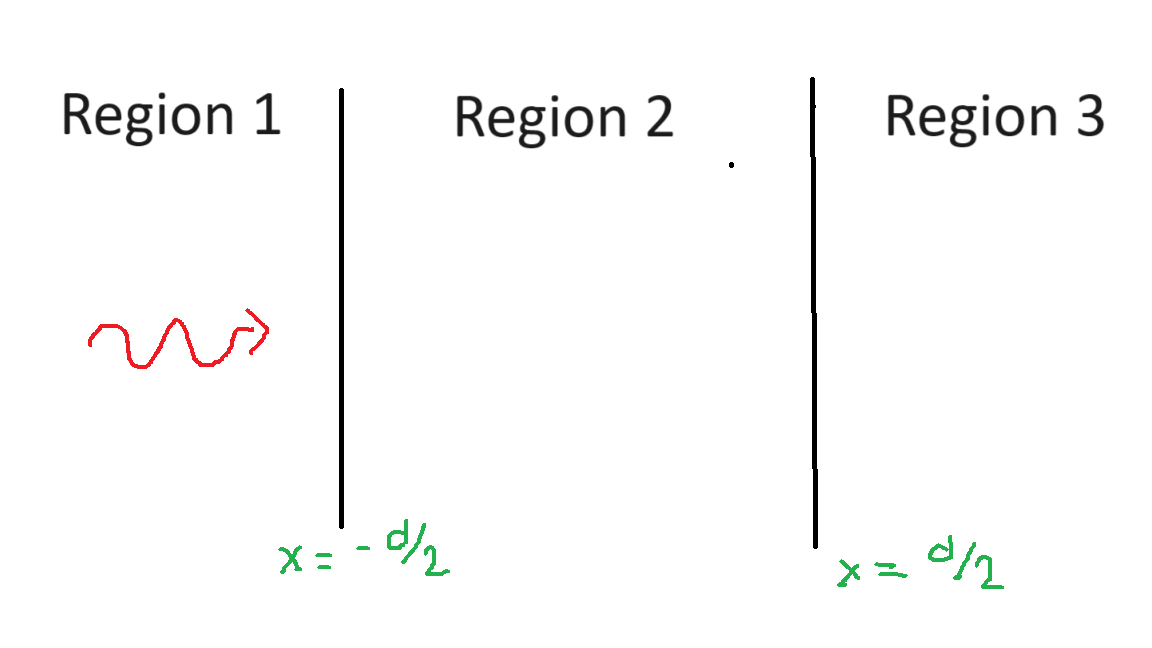
Consider a layered medium, which consists of three regions. Region i has a real, frequency-independent refractive index given by ni , where i = 1, 2, 3. The boundary interface between regions 1 and 2, which is located at x = ?d/2, is a resistive sheet of surface conductivity ?12. Likewise, the interface between regions 2 and 3 located at x = d/2 is another resistive sheet of conductivity ?23. The surface current density on a resistive sheet is given by Ohm's Law K = ?E?, where ? is the surface conductivity of the sheet and E? is the tangential component of the electric field at the surface. A plane wave is normally incident on the resistive sheet located at x = ?d/2 from region 1. This incident wave has an electric field amplitude E0 and is linearly polarized along the y-direction.

Hint: Consider the electromagnetic boundary conditions at the interface taking into account the presence of the resistive sheet. Note: All regions are non-magnetic with a magnetic permeability = 0.

\f(E-kix - wt ) no e y . Ex is cont at interface =0 IXEr - nig (( -kix - ut ) MIC - Eroe . It , is discont' at intaface *= 0 by Eto = Surface arment chasity K = 02 , nithz t loco MIC 7 1 (8. - Ero ) - 12 Ex = 5'2ro R = Ero -_ 1 - 12 - 4060 / 2 At X = 0 : - ( 2 ) 22 PERSONS . Solving (1J & (2 ) . Eol to CUCKEX -WE ) nit 12 + Hoco X x [ EE- ( E + Er ) = 0 n 2 Ero = Hic T= 12 2to = 1/2 20, i(kx - wt ) 12- Exo e - ) Eto = Eat Ero ( ) . Mic + 1 2 C 2 for Mi = MZ = Mo > E = 1 - R-T - fraction of every dissipated.