Consider a renewal process N(t) where T1, T2, . . . are i.i.d. and uniformly distributed

on [0, 1]. Derive the renewal function m(t) for t ? 1.

58 Consider a lamp where the lightbulbs are replaced either when they burn out or when

they have burned for 336 hours. The lifelengths of lightbulbs are assumed to be i.i.d.

and exponentially distributed with mean 300 hours. (a) How often are the lightbulbs

replaced in the long run? (b) What is the probability that a supply of 50 lightbulbs will

last for a year (8760 hours)?

59 M/G/1/114

. Assume that customers arrive to a service station with one server according

to a Poisson process with rate ?. When an arriving customer finds the service station

empty, he enters and starts being served, whereas if the server is busy, he leaves and

never returns. (a) If we denote the mean service time S, at what rate do customers

enter the service station? (b) What proportion of customers are actually served by the

service station?

60 Let us assume that ? = 5 customers per minute in the previous problem and that the

mean and variance of the service times are S = 0.25 and ?

2

S = 0.1, respectively.

What is the probability that at least 120 customers will be served during one hour?

61 Find the distribution Fe(t) of the initial inter-arrival time in a delayed renewal process

if the subsequent inter-arrival times are (a) Exponentially distributed (delayed Poisson

process). (b) Uniformly distributed on [0, 1]. (c) Gamma distributed with ? = 2

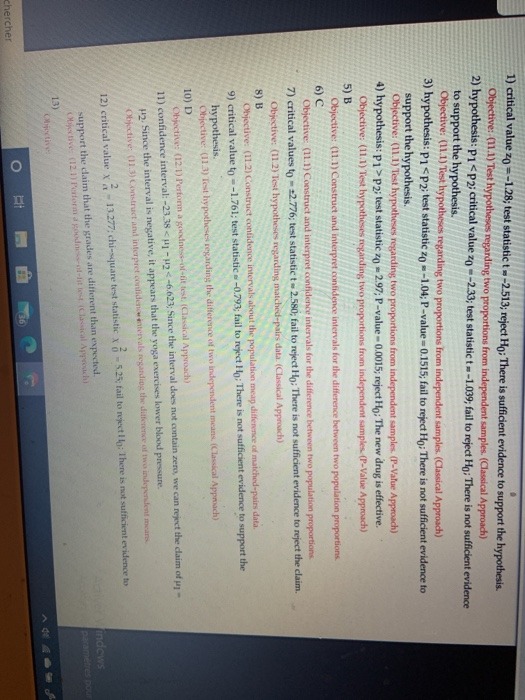
3, For two random variables X and Y, the joint probability density function is given by fxx(x, y) = Ce * Zu(x)u(y) Find: a. C b. Fxx (x, y), the joint cumulative distribution function. c. Fx(x) and Fy (y), marginal distribution functions d. Are X and Y independent?The following table shows the average hourly wage rates for day-care centers from two locations based on two random samples. Use the table to complete parts a through c. Location 1 Location 2 Sample mean $9.62 $8.59 Sample standard deviation $1.23 $1.11 Sample size 28 35 a. Perform a hypothesis test, using a =0.10, to determine if the average hourly wage for day-care workers in Location 1 is $0.50 per hour higher than the average hourly wage for day-care workers in Location 2. Assume the population variances for wage rates in each location are equal. Determine the null and alternative hypotheses for the test. Ho: 1 - H2 5 $0.50 H1: 1 - 12 > $0.50 Calculate the appropriate lost statistic and interpret the result. The test statistic is (Round to two decimal places as needed.) Enter your answer in the answer box and then click Check Answer.5. A random sample of 30 binomial trials resulted in 12 successes. Test the claim that the population proportion of successes does not equal 0.50. Use a level of significance of 0.05. a. Check requirements, is X distribution normal? Explain b. State the null and alternate hypothesis: c. Compute the sample test statistic: d. For H, estimate the P-value of the test statistic: e. Conclude the test: f. Interpret the results:1) critical value zo =-1.28; test statistic t =-2.513; reject Ho; There is sufficient evidence to support the hypothesis. Objective: (11.1) Test hypotheses regarding two proportions from independent samples. (Classical Approach) 2) hypothesis: p1 p2; test statistic zg = 2.97; P-value - 0.0015; reject Hy; The new drug is effective. Objective: (11.1) Test hypotheses regarding two proportions from independent samples. (P-Value Approach) 5) B Objective: (11.1) Construct and interpret confidence intervals for the difference between two population proportions. 6) C Objective: (11.1) Construct and interpret confidence intervals for the difference between two population proportions 7) critical values to - 2.776; test statistic to 2.580, fail to reject Hy; There is not sufficient evidence to reject the claim. Objective: (11.2) Tou hypotheses regarding matched-pairs data. (Classical Approach) 8) B Objective: (11 2) Construct confidence intervals about the population mean difference of maiched-pairs data. 9) critical value to - -1.761; test statistic - -0.793; fail to reject Hy; There is not sufficient evidence to support the hypothesis. Objective: (11 3) Test hypotheses regarding the difference of two independent means. (Classical Approach) 10) D Objective: (12,1) Pertonn a goodness-of-fit test. (Classical Approach) 11) confidence interval: -23 38