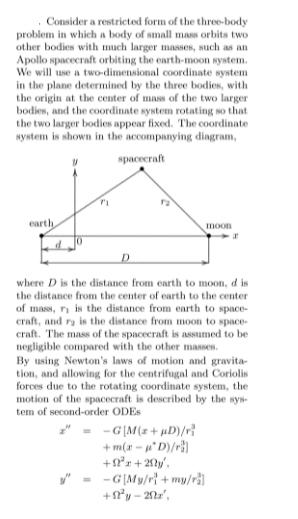
Consider a restricted form of the three-body problem in which a body of small mass orbits two other bodies with much larger masses, such as an Apollo spacecraft orbiting the earth-moon system. We will use a two-dimensional coordinate system in the plane determined by the three bodies, with the origin at the center of mass of the two larger bodies, and the coordinate system rotating so that the two larger bodies appear fixed. The coordinate system is shown in the accompanying diagram, earth, d spacecraft D moon where D is the distance from earth to moon, d is the distance from the center of earth to the center of mass, r, is the distance from earth to space- craft, and ry is the distance from moon to space- craft. The mass of the spacecraft is assumed to be negligible compared with the other masses. By using Newton's laws of motion and gravita- tion, and allowing for the centrifugal and Coriolis forces due to the rotating coordinate system, the motion of the spacecraft is described by the sys tem of second-order ODES -GIM(z+D)/r +m(a-D)/r +9 +20 =-G My/r+my/rl +y-20tz, a where G is the gravitational constant, M and m are the masses of earth and moon, p and are the mass fractions of earth and moon, and ? is the angular velocity of rotation of the moon about the earth (and hence of the coordinate system). The numerical values of these quantities are given in the following table: G M m #4 # D d 71 6.67259 x 10 m/(kg ) 5.974 x 1024 kg 7.348 x 10 kg M/(m + M) m/(m + M) 3.844 x 10 m 4.669 x 10 m. [(x+d) + /2 (D-d-a)+ya 52 2.661 x 10 / Use a library routine to solve this system of ODES with the initial conditions (0)-4.613 x 10, z(0)=0. v(0) -0. v (0) = -1074. Plot the resulting solution trajectory (z(t), y(t)) in the plane as a function of time. Indicate the positions of earth and moon on the graph. Com- pute the solution for at least one complete orbit (i.e., until the spacecraft returns to its original lo cation), which is from t= 0 until approximately t = 2.4 x 10 s. Experiment with various error tolerances to see how much difference they make in whether the orbit is actually closed. Try to monitor the step size used by the ODE routine as the integration progresses. When does the step size become smaller or larger? How close does the spacecraft come to the surface of earth? (Earth's radius is 6.378 x 10 m, so the center of mass of the earth-moon system is actually inside the earth.)