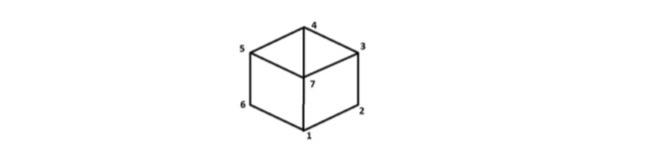
Consider a simple random walk {Xn} n0 in the graph below starting at point 1,

ie X0 = 1 and in each step we uniformly select one of the neighbors, eg P (1, 7) = 1/3.

a) (3 points) Is the Markov chain {Xn} irreducible?

b) (4 points) Is it aperiodic?

c) (4 points) Which statement is true: 'has no stationary measure', 'has the only stationary measure', 'has more than one stationary measure'?

d) (4 points) Does the Xn distribution converge to some distribution?

e) Additional problem (10 points). Let us assume that X0 has the distribution p1 + (1 - p) 2 for p (0, 1), i.e.

P [X0 = 1] = p and P [X0 = 2] = 1 - p. Does the distribution Xn converge to some distribution?

f) (10 points) What will be the answers to questions a) - d) for a simple random walk on the following page

graph?

In detail