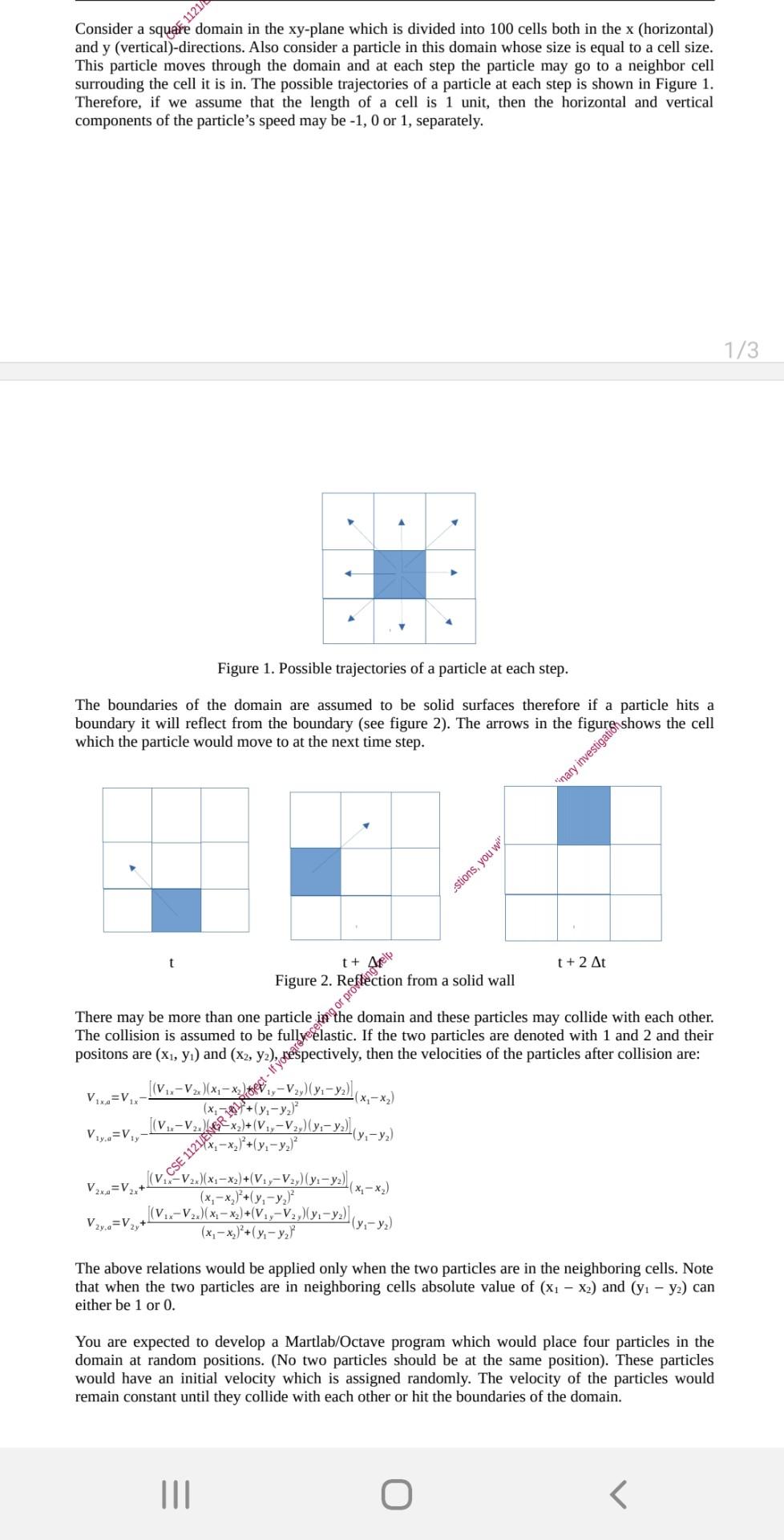
Consider a square domain in the xy-plane which is divided into 100 cells both in the x (horizontal) and y (vertical)-directions. Also consider a particle in this domain whose size is equal to a cell size. This particle moves through the domain and at each step the particle may go to a neighbor cell surrouding the cell it is in. The possible trajectories of a particle at each step is shown in Figure 1. Therefore, if we assume that the length of a cell is 1 unit, then the horizontal and vertical components of the particle's speed may be 1,0 or 1 , separately. Figure 1. Possible trajectories of a particle at each step. The boundaries of the domain are assumed to be solid surfaces therefore if a particle hits a boundary it will reflect from the boundary (see figure 2). The arrows in the figurghows the cell which the particle would move to at the next time step. positons are (x1,y1) and (x2,y2), resspectively, then the velocities of the particles after collision are: V2x,0=V2x+(x1x2)2+(y1y2)2[(V1,xCV2x)(x1x2)+(V1yV2y)(y1y2)](x1x2)V2y,a=V2y+(x1x2)2+(y1y2)2[(V1xV2x)(x1x2)+(V1yV2y)(y1y2)](y1y2) The above relations would be applied only when the two particles are in the neighboring cells. Note that when the two particles are in neighboring cells absolute value of (x1x2) and (y1y2) can either be 1 or 0. You are expected to develop a Martlab/Octave program which would place four particles in the domain at random positions. (No two particles should be at the same position). These particles would have an initial velocity which is assigned randomly. The velocity of the particles would remain constant until they collide with each other or hit the boundaries of the domain. Your program is to simulate the motion of the particles as a function of time. For this purpose the partices would be presented with square symbols on an xy-plot and the position of a particle will be updated according to: xnew=x+Vxtynew=y+Vyt where the time step t is equal to 1 . After the positions of the particles are updated the figure should be updated also. Note that there should be only one figure showing the current positions of the particles. The simulation should be made for 100 time steps. You may consider using the "pause" function for better visualization. Recording the positions of the particles, your program should create a second figure which plots the trajectories of the particles. The program should also write the x,y positions of particles as a function of time in to text files as a table with suitable column headers. The total displacement of the particleshould also be written at the end of the file. Data of each particle will be written in to a different fife. The figures and the output files should be self-sufficient, i.e., they should contain all the necessary explanations. The program may contain a main script and user-defined, fnctions