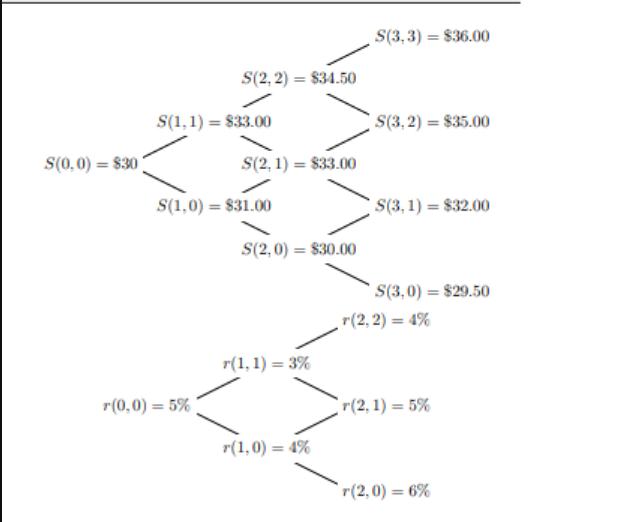
Consider a three-step binomial model. The stock prices S(n.j) and interest rates r(n, j) are shown in the two binomial pricing trees below. S(0,0) = 830) S(2, 2) = $34.50 S(1,1)= $33.00 r(0,0) = 5% S(2, 1) = $33.00 S(1,0) = $31.00 S(2,0) = $30.00 r(1,1)= 3% r(1,0) = 4% S(3, 3) = $36.00 S(3,2) = $35.00 S(3,1) = $32.00 S(3,0) = $29.50 r(2, 2) = 4% r(2, 1) = 5% r(2,0) = 6% (a) Verify that there is no arbitrage opportunity at any time. (b) Calculate the forward price and future price for forward and future contracts maturing at time N = 3 and begun at node (n.j), with n = 0, 1, 2, 3 and 0 jn. (c) Although interest rates are stochastic, you should find that G(2.j) = F(2.j) for all j= 0,1,2. Why is this? (d) Make the interest rate deterministic with r(0) = 0.05, r(1) = 0.03 and r(2)= 0.04 and show that the forward and future prices are now equal.