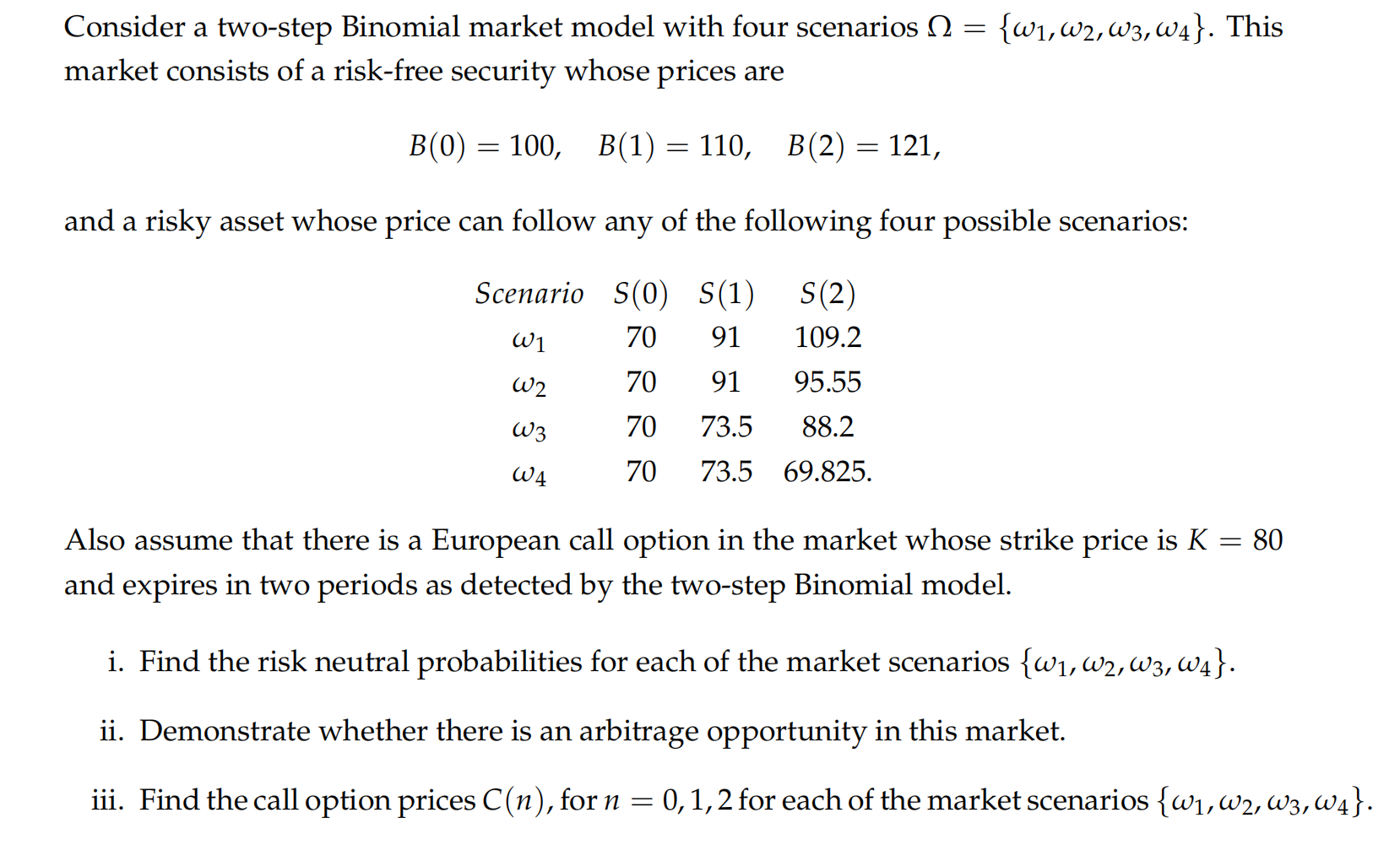
Consider a two-step Binomial market model with four scenarios = {1, 2, 3, 4}. This

market consists of a risk-free security whose prices are

B(0) = 100,

B(1) = 110,

B(2) = 121,

and a risky asset whose price can follow any of the following four possible scenarios:

Scenario S(0) S(1)

S(2)

1

70 91 109.2

2

70 91 95.55

3

70 73.5 88.2

4

70 73.5 69.825.

Also assume that there is a European call option in the market whose strike price is K = 80

and expires in two periods as detected by the two-step Binomial model.

i. Find the risk neutral probabilities for each of the market scenarios {1, 2, 3, 4}.

ii. Demonstrate whether there is an arbitrage opportunity in this market.

iii. Find the call option prices C(n), for n = 0, 1, 2 for each of the market scenarios {1, 2, 3, 4}

Consider a two-step Binomial market model with four scenarios Q = {W1,W2,63,W4}. This market consists of a risk-free security whose prices are B(0) = 100, B(1) = 110, B(2) = 121, and a risky asset whose price can follow any of the following four possible scenarios: Scenario S(0) S(1) S(2) W1 70 91 109.2 W2 70 91 95.55 W3 70 73.5 88.2 70 73.5 69.825. W4 Also assume that there is a European call option in the market whose strike price is K = 80 and expires in two periods as detected by the two-step Binomial model. i. Find the risk neutral probabilities for each of the market scenarios {W1,W2,W3,W4}. ii. Demonstrate whether there is an arbitrage opportunity in this market. iii. Find the call option prices C(n), for n = 0,1,2 for each of the market scenarios {W1,W2, W3,W4}. Consider a two-step Binomial market model with four scenarios Q = {W1,W2,63,W4}. This market consists of a risk-free security whose prices are B(0) = 100, B(1) = 110, B(2) = 121, and a risky asset whose price can follow any of the following four possible scenarios: Scenario S(0) S(1) S(2) W1 70 91 109.2 W2 70 91 95.55 W3 70 73.5 88.2 70 73.5 69.825. W4 Also assume that there is a European call option in the market whose strike price is K = 80 and expires in two periods as detected by the two-step Binomial model. i. Find the risk neutral probabilities for each of the market scenarios {W1,W2,W3,W4}. ii. Demonstrate whether there is an arbitrage opportunity in this market. iii. Find the call option prices C(n), for n = 0,1,2 for each of the market scenarios {W1,W2, W3,W4}