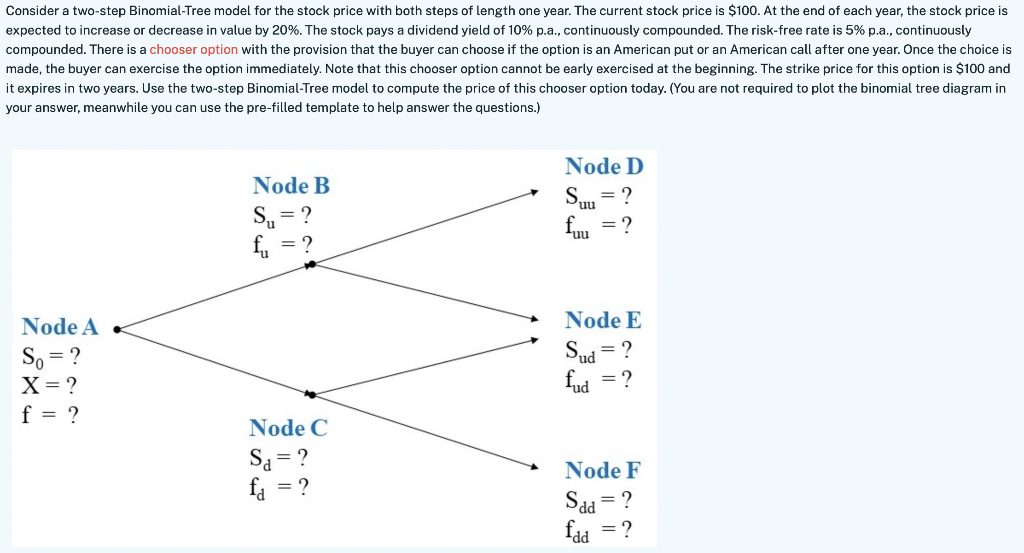
Consider a two-step Binomial-Tree model for the stock price with both steps of length one year. The current stock price is $100. At the end of each year, the stock price is expected to increase or decrease in value by 20%. The stock pays a dividend yield of 10% p.a., continuously compounded. The risk-free rate is 5% p.a., continuously compounded. There is a chooser option with the provision that the buyer can choose if the option is an American put or an American call after one year. Once the choice is made, the buyer can exercise the option immediately. Note that this chooser option cannot be early exercised at the beginning. The strike price for this option is $100 and it expires in two years. Use the two-step Binomial-Tree model to compute the price of this chooser option today. (You are not required to plot the binomial tree diagram in your answer, meanwhile you can use the pre-filled template to help answer the questions.) Node B Su = ? fi = ? Node D Suu = ? fuu = ? Node A So = ? X = ? f = ? Node E Sud = ? fud = ? Node C Sa= ? fa = ? Node F Sda = ? fad = ? The given information SO=100, X=100, r=5%, q = 10%, u=1.2, d=0.8, in each step T=1 Step 1: We can compute the risk-neutral probability: Step 2: In a two-step binomial tree, we know the following (You can delete this step 2 if you run out of space) At Node A: SO = 100, X=100, f to be computed in later steps At Node B: Su=120, fu to be computed in later steps At Node C: Sd=80, fd to be computed in later steps At Node D: Suu=144, fuu depends on whether it is a call or put At Node E: Sud=96, fud depends on whether it is a call or put At Node F: Sdd=64, fdd depends on whether it is a call or put Step 3 In the right-upper branch, if it is a call option, fuu=?, fud=? In the right-upper branch, if it is a put option, fuu=?, fud=? The option value at Node B is fu=? (Hint: you will need to consider possible early exercise for both American call and put in this case since the stock pays dividend. The early exercise payoff is simply the difference between the stock price and the strike price at that certain Node, and the order depends on whether it is a call or a put). Consider a two-step Binomial-Tree model for the stock price with both steps of length one year. The current stock price is $100. At the end of each year, the stock price is expected to increase or decrease in value by 20%. The stock pays a dividend yield of 10% p.a., continuously compounded. The risk-free rate is 5% p.a., continuously compounded. There is a chooser option with the provision that the buyer can choose if the option is an American put or an American call after one year. Once the choice is made, the buyer can exercise the option immediately. Note that this chooser option cannot be early exercised at the beginning. The strike price for this option is $100 and it expires in two years. Use the two-step Binomial-Tree model to compute the price of this chooser option today. (You are not required to plot the binomial tree diagram in your answer, meanwhile you can use the pre-filled template to help answer the questions.) Node B Su = ? fi = ? Node D Suu = ? fuu = ? Node A So = ? X = ? f = ? Node E Sud = ? fud = ? Node C Sa= ? fa = ? Node F Sda = ? fad = ? The given information SO=100, X=100, r=5%, q = 10%, u=1.2, d=0.8, in each step T=1 Step 1: We can compute the risk-neutral probability: Step 2: In a two-step binomial tree, we know the following (You can delete this step 2 if you run out of space) At Node A: SO = 100, X=100, f to be computed in later steps At Node B: Su=120, fu to be computed in later steps At Node C: Sd=80, fd to be computed in later steps At Node D: Suu=144, fuu depends on whether it is a call or put At Node E: Sud=96, fud depends on whether it is a call or put At Node F: Sdd=64, fdd depends on whether it is a call or put Step 3 In the right-upper branch, if it is a call option, fuu=?, fud=? In the right-upper branch, if it is a put option, fuu=?, fud=? The option value at Node B is fu=? (Hint: you will need to consider possible early exercise for both American call and put in this case since the stock pays dividend. The early exercise payoff is simply the difference between the stock price and the strike price at that certain Node, and the order depends on whether it is a call or a put)