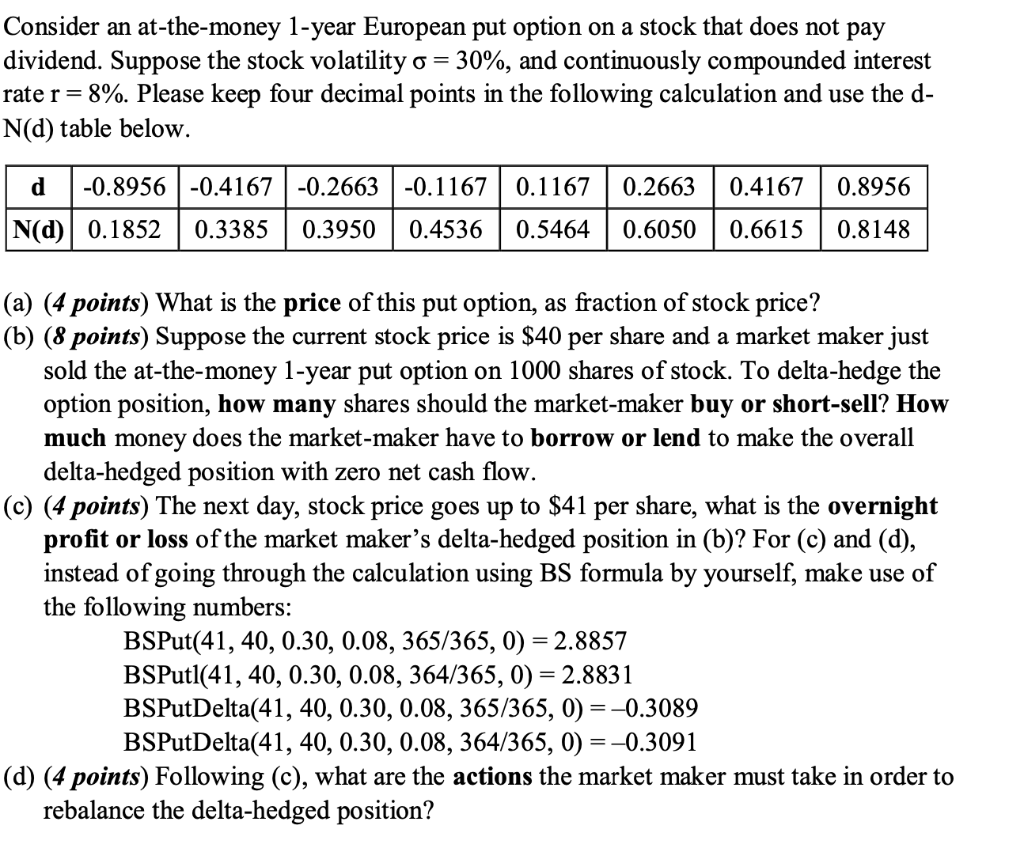
Consider an at-the-money 1-year European put option on a stock that does not pay dividend. Suppose the stock volatility o= 30%, and continuously compounded interest rate r = 8%. Please keep four decimal points in the following calculation and use the d- N(d) table below. d -0.8956 -0.4167 -0.2663 -0.1167 0.1167 0.2663 0.4167 0.8956 N(d) 0.1852 0.3385 0.3950 0.4536 0.5464 0.6050 0.6615 0.8148 (a) (4 points) What is the price of this put option, as fraction of stock price? (b) (8 points) Suppose the current stock price is $40 per share and a market maker just sold the at-the-money 1-year put option on 1000 shares of stock. To delta-hedge the option position, how many shares should the market-maker buy or short-sell? How much money does the market-maker have to borrow or lend to make the overall delta-hedged position with zero net cash flow. (c) (4 points) The next day, stock price goes up to $41 per share, what is the overnight profit or loss of the market maker's delta-hedged position in (b)? For (c) and (d), instead of going through the calculation using BS formula by yourself, make use of the following numbers: BSPut(41, 40, 0.30, 0.08, 365/365, 0) = 2.8857 BSPutl(41, 40, 0.30, 0.08, 364/365, 0) = 2.8831 BSPutDelta(41, 40, 0.30, 0.08, 365/365, 0) =-0.3089 BSPutDelta(41, 40, 0.30, 0.08, 364/365, 0) =-0.3091 (d) (4 points) Following (c), what are the actions the market maker must take in order to rebalance the delta-hedged position? Consider an at-the-money 1-year European put option on a stock that does not pay dividend. Suppose the stock volatility o= 30%, and continuously compounded interest rate r = 8%. Please keep four decimal points in the following calculation and use the d- N(d) table below. d -0.8956 -0.4167 -0.2663 -0.1167 0.1167 0.2663 0.4167 0.8956 N(d) 0.1852 0.3385 0.3950 0.4536 0.5464 0.6050 0.6615 0.8148 (a) (4 points) What is the price of this put option, as fraction of stock price? (b) (8 points) Suppose the current stock price is $40 per share and a market maker just sold the at-the-money 1-year put option on 1000 shares of stock. To delta-hedge the option position, how many shares should the market-maker buy or short-sell? How much money does the market-maker have to borrow or lend to make the overall delta-hedged position with zero net cash flow. (c) (4 points) The next day, stock price goes up to $41 per share, what is the overnight profit or loss of the market maker's delta-hedged position in (b)? For (c) and (d), instead of going through the calculation using BS formula by yourself, make use of the following numbers: BSPut(41, 40, 0.30, 0.08, 365/365, 0) = 2.8857 BSPutl(41, 40, 0.30, 0.08, 364/365, 0) = 2.8831 BSPutDelta(41, 40, 0.30, 0.08, 365/365, 0) =-0.3089 BSPutDelta(41, 40, 0.30, 0.08, 364/365, 0) =-0.3091 (d) (4 points) Following (c), what are the actions the market maker must take in order to rebalance the delta-hedged position