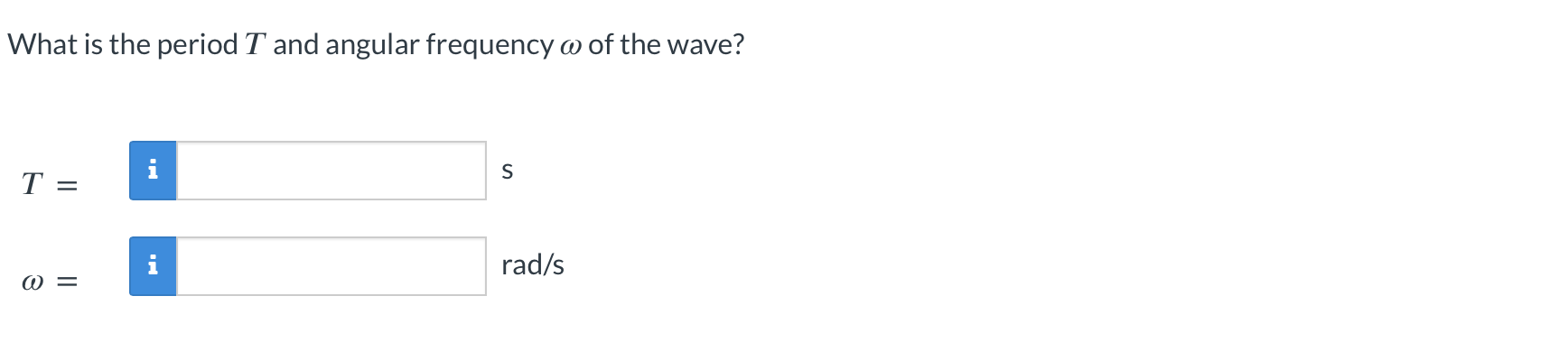
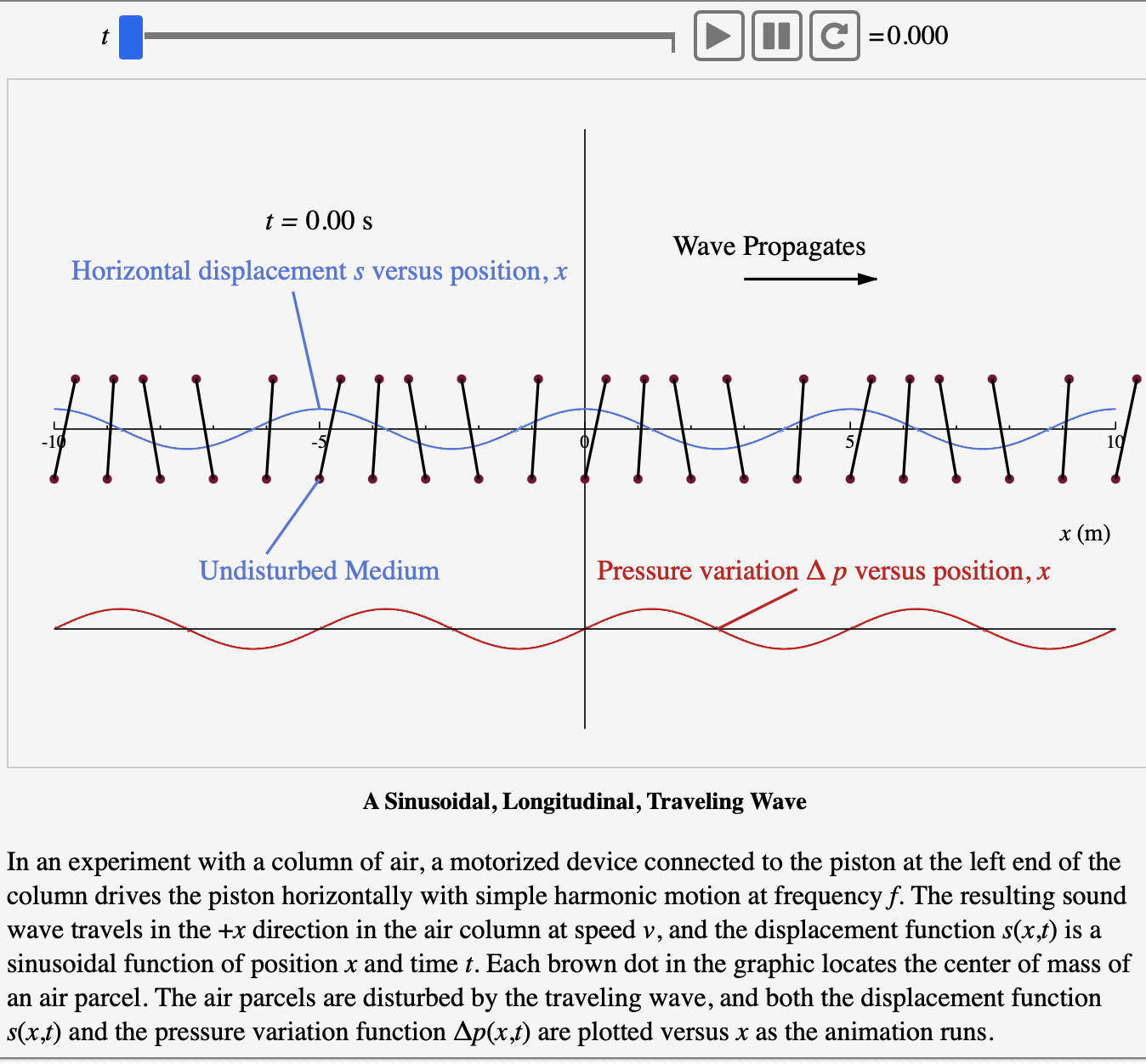
Consider an experiment with the air column in Fig. 17.4.1. A motorized device connected to the piston at the left end of the column drives the piston horizontally with simple harmonic motion at frequency f. The resulting sound wave travels in the + x direction in the air column at speed v, and the displacement function s(x, t) is a sinusoidal function of position x and time t. We shall assume the displacement function has the following generic form: s(x, t) = Sm cos (kx wt + p) This piston can move horizontally. parcel of air in equilibrium location: x +x (cm) x = 0 10 20 Air pressure is uniform in pipe with value Patm Interactive Figure 17.4.1: Air in a long, cylindrical pipe has uniform density and pressure before the piston at the left end creates any disturbance. Take Note: (A) Equation (A) is an important relationship in Chapter 17. It is a sinusoidal traveling wave with displacement amplitude Sm. The equation is the same form as we came across in Chapter 16 when we studied traveling waves on a taut string. Other properties of this wave to note are: The argument of the cosine function, kx wt + & is called the phase of the cosine function. The phase has SI units of radians. k is called the angular wave number (SI units: rad/m). k tells us how much the phase of the cosine function changes in radians for every meter along the x axis. The angular wave number is related to the wavelength through the relationship k = 2/ w is called the angular frequency (SI units: rad/s). w tells us how much the phase of the cosine function changes in radians for every second that transpires on the clock. The angular frequency is related to the period T through the relationship w = 2/. The speed v of the wave can be computed from @ and k: v = w/k. Simulation A Sinusoidal, Longitudinal, Traveling Wave For a sound wave traveling in the + x direction, the phase takes the form kx - wt + while for a sound wave traveling in the - x direction, the phase takes the form kx + wt + = is called the phase angle (SI units: rad). tells us the displacement att = O of the parcel that lies at x s(0,0) = = Sm cos(p) The next exercises provide practice applying Eq. (A). A sinusoidal sound wave is depicted in the simulation (linked below). Run the animation now. O when in equilibrium: What is the period T and angular frequency of the wave? T = @= S rad/s What is the speed u of the wave? V = i m/s t t = 0.00 s Horizontal displacement s versus position, x IC=0.000 Undisturbed Medium Wave Propagates / \ \ \ / / / \ \ / / / \ \ / / | \\ H -10 Pressure variation A p versus position, x x (m) A Sinusoidal, Longitudinal, Traveling Wave In an experiment with a column of air, a motorized device connected to the piston at the left end of the column drives the piston horizontally with simple harmonic motion at frequency . The resulting sound wave travels in the +x direction in the air column at speed v, and the displacement function s(x,t) is a sinusoidal function of position x and time t. Each brown dot in the graphic locates the center of mass of an air parcel. The air parcels are disturbed by the traveling wave, and both the displacement function s(x,t) and the pressure variation function Ap(x,t) are plotted versus x as the animation runs.