Question
Consider an individual facing the prospect of having high income, yH > 0, with probability H, medium income of yM with probability M and low
Consider an individual facing the prospect of having high income, yH > 0, with probability H, medium income of yM with probability M and low income, yL, with probability L, yH > yM > yL. Let the individuals preferences be represented by a utility function that is defined on consumption of a consumption good, u(c). The utility function represents preferences such that more is better, u0(c) > 0, features diminishing marginal utility of consumption, u00(c)
limc!0 u0(c) = infinite. Assume, for simplicity, that income is paid in units of consumption goods.
Prior to learning the realization of income, the individual has w units of wealth to spend on aquiring assets. This wealth cannot be stored nor consumed to provide utility. There are two types of assets that the individual can buy or sell. Each unit of Asset 1 costs q1 units of wealth and pays a single unit of the consumption good per asset purchased only if income is realized to be high. In contrast, the individual must pay q2 units of wealth per unit of Asset 2. Each unit of Asset 2 held by the individual yields R units of the consumption good if income is realized to be yH, yM or yL. Let a1 denote the units of Asset 1 purchased by the individual while a2 denotes the number of Asset 2 purchased by the individual. Negative values of a1 or a2 mean that the individual is selling rather than purchasing assets.
Formally, the individuals problem is to maximize the expected utility from consumption subject to the constraints that consumption must be financed out of income and the realized return from the asset portfolio as well as a constraint that spending on the asset portfolio must be financed out of the non-storable endowment wealth w.
max {H u(cH ) + M u(cM ) + Lu(cL)}
cH ,cM ,cL ,a1 ,a2
cH =yH+a1+Ra2 (1)
cM =yM+Ra2 (2)
cL =yL+Ra2 (3)
w = q1a1 + q2a2. (4)
Denote the optimal allocation by (cH , cM , cL, a1, a2). 1 H u 0 ( c H ) = 1 R [ H u 0 ( c H ) + M u 0 ( c M ) + L u 0 ( c L ) ] . (5)
-
Using words, interpret the optimal trade-o condition of equation (5) and why the optimal portfolio plan must satisfy this condition. Make sure that you explain the economic trade-o, dont simply list the terms on both sides of the equality sign. You might need to make reference to equations (1) through equation (4) in describing the costs and benefits of any feasible portfolio reallocations.
-
Do the asset return structures give the individual the opportunity to fully insure against consumption risk? Explain why (or why not).
-
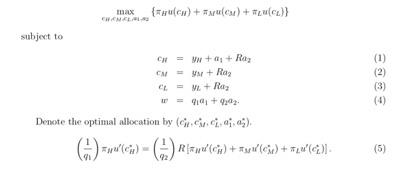
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


