Consider an n-

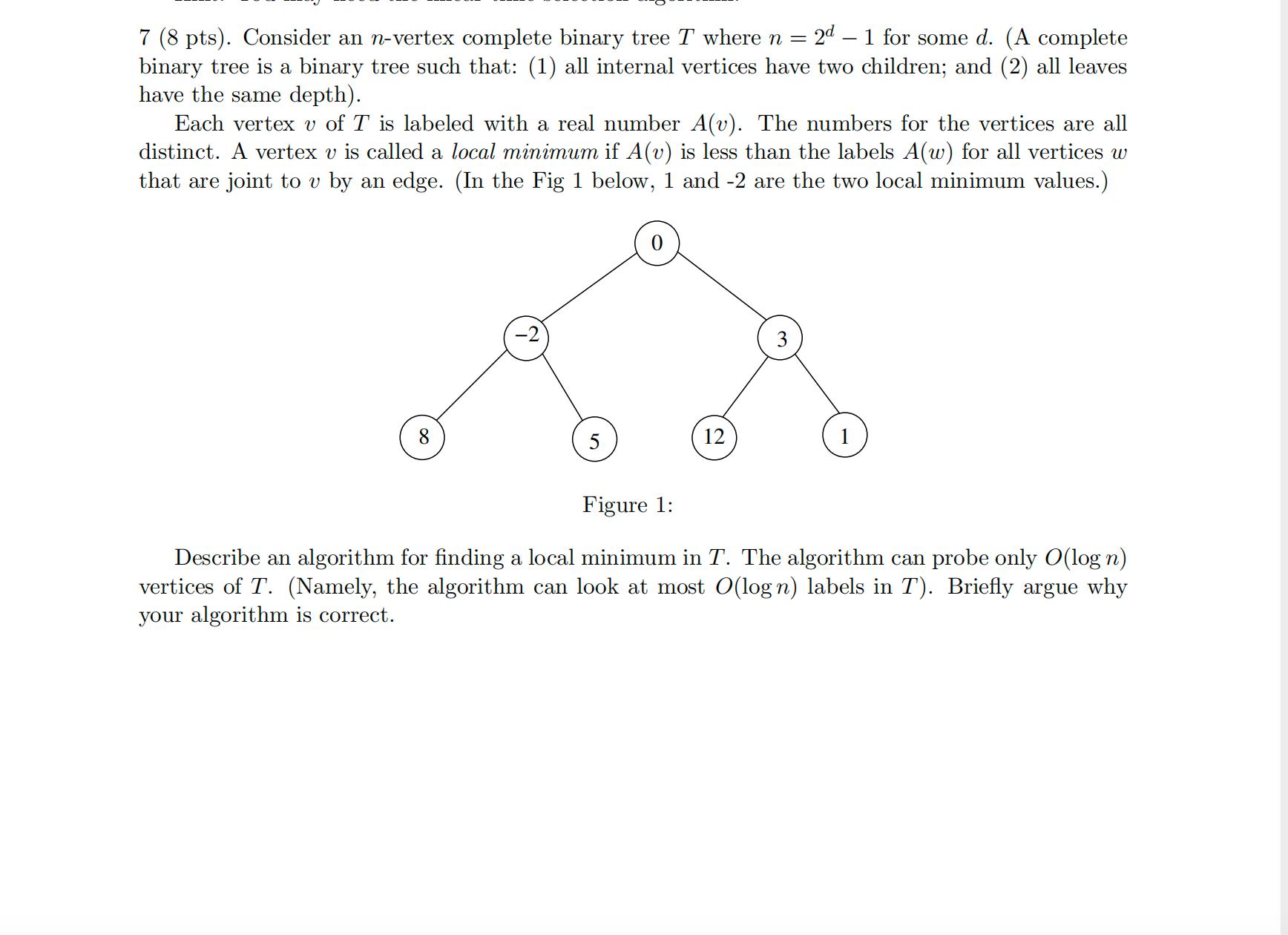
7 (8 pts). Consider an n-vertex complete binary tree T where n = 2d - 1 for some d. (A complete binary tree is a binary tree such that: (1) all internal vertices have two children; and (2) all leaves have the same depth). Each vertex v of T is labeled with a real number A(v). The numbers for the vertices are all distinct. A vertex v is called a local minimum if A(v) is less than the labels A(w) for all vertices w that are joint to v by an edge. (In the Fig 1 below, 1 and -2 are the two local minimum values.) 8 5 12 1 Figure 1: Describe an algorithm for finding a local minimum in T. The algorithm can probe only O(log n) vertices of T. (Namely, the algorithm can look at most O(logn) labels in T). Briefly argue why your algorithm is correct.