Question
Consider the case where a monopolist's inverse demand function equals P = 30 -2Q, and the firm's total costs are given by C(Q) = (1/2)Q2,
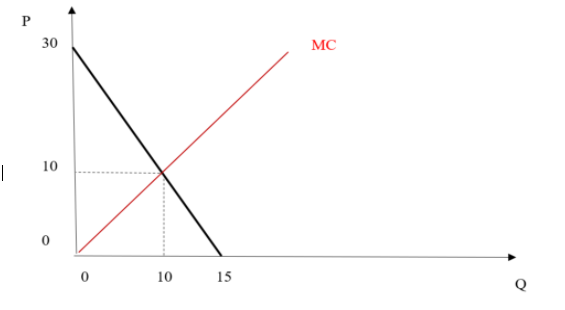
Consider the case where a monopolist's inverse demand function equals P = 30 -2Q, and the firm's total costs are given by C(Q) = (1/2)Q2, which results in a marginal cost equal to Q. The following illustration depicts the output that maximizes total surplus. This output is economically efficient.
Total Surplus is maximized when the firm produces 10 units. Total surplus equals $150 when output equals 10.The total amount consumers are willing to pay (WTP) for 10 units of the good equals the area under the demand curve.WTP (10) = 10 x 10 + (1/2) (30 - 10) x 10 = 100 + 100 = $200
The total variable cost of producing 10 units equals the area underneath the marginal-cost curve, which equals (1/2) x 10 x 10 = $50
The different between WTP and variable cost equals total surplus. WTP - TVC = $200 - $50 = $150.The single-price monopolist maximizes profit by producing 6 units and setting price equals to $18. The monopolist's profit equals $90. The single-price monopolist only captures 60 percent of the total surplus available in this market.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


