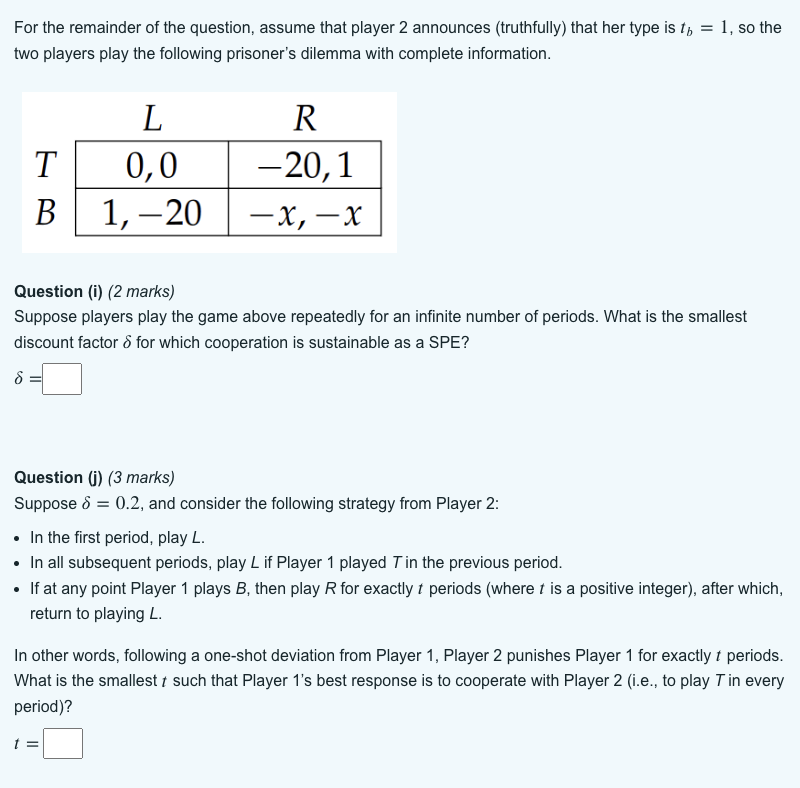
Consider the following Bayesian game. Player 2 can be of type t = {a, b} where Pr(t = a) = . Player 2 knows his type, but Player 1 only knows the prior distribution of 2's type. If Player 2 is of type a, then the payoffs are given by the matrix L R T X, X 0,0 B 0,0 1,1 while if Player 2 is of type b, then the payoffs are given by the matrix L R T 0,0 -20,1 B 1,-20 -x,-x where x = 14. Put differently, Player 1 does not know whether they are playing a coordination game, or a prisoner's dilemma. Call Player 2's probability of playing L if he is of type a, Player 2's probability of playing L if he is of type b, and T Player 1's probability of playing T. Throughout this question, if your answer is a decimal number you should round to 3 decimal places. E.g. if you find the answer to be "0.87352", please input "0.874" in the answer box. Question (a) (0.5 marks) Suppose Player 1 chooses T = 0. Player 2's best response is a when t = b. Question (b) (0.5 marks) Suppose and are as in (a). Then Player 1's best response is T = a Question (c) (0.5 marks) when ta, and = Suppose Player 1 chooses T = 1. Player 2's best response is = when t = b. when ta, and = Question (d) (0.5 marks) Suppose and are as in (c). Then Player 1's best response is T = Question (e) (1 mark) Is there a Bayesian Nash equilibrium in which T = 0? If so, what are the values of a and in this equilibrium (if no such equilibrium exists, input "-1" as the value for both and )? b = Question (f) (1 mark) Is there a Bayesian Nash equilibrium in which T = 1? If so, what are the values of and in this equilibrium (if no such equilibrium exists, input "-1" as the value for both and )? = b = Now we consider the possibility of mixed-strategy Bayesian Nash equilibria. Question (g) (1 mark) In any Bayesian Nash equilibrium (mixed or otherwise), = Question (h) (3 marks) Hence the unique Bayesian Nash equilibrium in which at least one player plays a mixed strategy is given by T = For the remainder of the question, assume that player 2 announces (truthfully) that her type is t = 1, so the two players play the following prisoner's dilemma with complete information. L R T 0,0 -20,1 B 1,-20 -x,-x Question (i) (2 marks) Suppose players play the game above repeatedly for an infinite number of periods. What is the smallest discount factor & for which cooperation is sustainable as a SPE? 8 = Question (j) (3 marks) Suppose = 0.2, and consider the following strategy from Player 2: In the first period, play L. In all subsequent periods, play L if Player 1 played 7 in the previous period. If at any point Player 1 plays B, then play R for exactly t periods (where t is a positive integer), after which, return to playing L. In other words, following a one-shot deviation from Player 1, Player 2 punishes Player 1 for exactly / periods. What is the smallest t such that Player 1's best response is to cooperate with Player 2 (i.e., to play T in every period)?