Question

1 Approved Answer

Posted on Oct 06, 2024

Consider the following data relating to a particular project. Initial Cost ($) Annual Labor Cost ($) Annual Maintenance Cost ($) Other Annual Costs ($) Variable

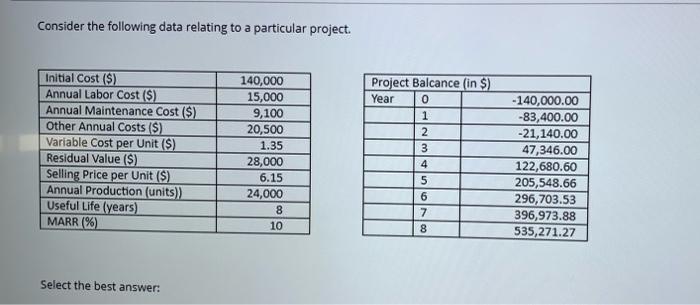
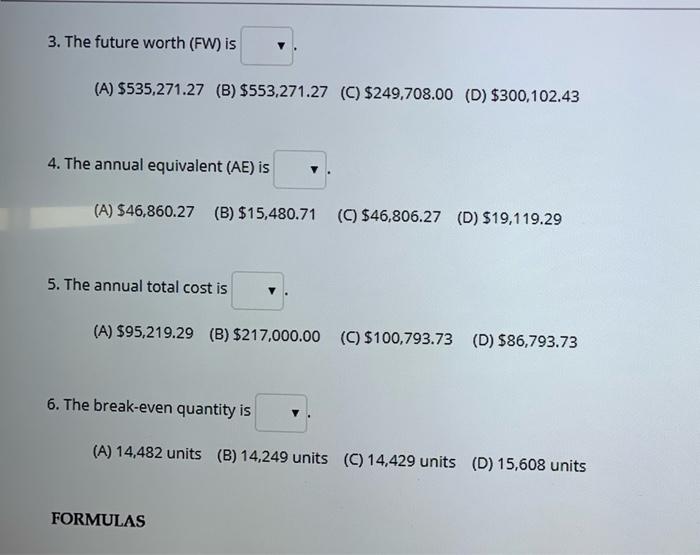
Consider the following data relating to a particular project. Initial Cost ($) Annual Labor Cost ($) Annual Maintenance Cost ($) Other Annual Costs ($) Variable Cost per Unit ($) Residual Value ($) Selling Price per Unit ($) Annual Production (units)) Useful Life (years) MARR (%) 140,000 15,000 9,100 20,500 1.35 28,000 6.15 24,000 8 10 Project Balcance (in $) Year 0 1 2 3 4 -140,000.00 -83,400.00 -21,140.00 47,346.00 122,680.60 205,548.66 296,703.53 396,973.88 535,271.27 5 6 7 8 Select the best answer: Select the best answer: 1. The discounted payback period is (A) 3.7 years (B) 2.3 years (C) 3.3 years (D) 2 years 2. The compound annual growth rate (CAGR) is (A) 8.2596 (B) 7.1496 (C) 48.7396 (D) 18.2596 3. The future worth (FW) is V (A) $535,271.27 (8) $553,271.27 (C) $249,708.00 (D) $300,102.43 4. The annual equivalent (AE) is (A) $46,860.27 (B) $15,480.71 (C) $46,806.27 (D) $19,119.29 5. The annual total cost is (A) $95,219.29 (B) $217,000.00 (C) $100,793.73 (D) $86,793.73 6. The break-even quantity is (A) 14,482 units (B) 14,249 units (C) 14,429 units (D) 15,608 units FORMULAS FORMULAS F = P(1+1) (1+1) PE (0*)** i= -1 P= F(1+1) -F (1+1) P=A ((1+1N1 i(1+1 N log() log(1+1) A=F La+n Depreciation - (Initial Cost - Residual Value) Interest on Capital - Initial Cost x interest A =p (1+1) (1+1)-1 FORMULAS F = P(1 +1) (1+1)^-1 F=4 P=F(1+1) F (1 +1) P=4 [(1+1N1 i(1+1). V N = log(4) log(1+1) i A=F ( (1+1)-1 Depreciation - (Initial Cost - Residual Value) x -1 Interest on Capital - Initial Cost x interest i(1+1) A=P (1+1)-1 Consider the following data relating to a particular project. Initial Cost ($) Annual Labor Cost ($) Annual Maintenance Cost ($) Other Annual Costs ($) Variable Cost per Unit ($) Residual Value ($) Selling Price per Unit ($) Annual Production (units)) Useful Life (years) MARR (%) 140,000 15,000 9,100 20,500 1.35 28,000 6.15 24,000 8 10 Project Balcance (in $) Year 0 1 2 3 4 -140,000.00 -83,400.00 -21,140.00 47,346.00 122,680.60 205,548.66 296,703.53 396,973.88 535,271.27 5 6 7 8 Select the best answer: Select the best answer: 1. The discounted payback period is (A) 3.7 years (B) 2.3 years (C) 3.3 years (D) 2 years 2. The compound annual growth rate (CAGR) is (A) 8.2596 (B) 7.1496 (C) 48.7396 (D) 18.2596 3. The future worth (FW) is V (A) $535,271.27 (8) $553,271.27 (C) $249,708.00 (D) $300,102.43 4. The annual equivalent (AE) is (A) $46,860.27 (B) $15,480.71 (C) $46,806.27 (D) $19,119.29 5. The annual total cost is (A) $95,219.29 (B) $217,000.00 (C) $100,793.73 (D) $86,793.73 6. The break-even quantity is (A) 14,482 units (B) 14,249 units (C) 14,429 units (D) 15,608 units FORMULAS FORMULAS F = P(1+1) (1+1) PE (0*)** i= -1 P= F(1+1) -F (1+1) P=A ((1+1N1 i(1+1 N log() log(1+1) A=F La+n Depreciation - (Initial Cost - Residual Value) Interest on Capital - Initial Cost x interest A =p (1+1) (1+1)-1 FORMULAS F = P(1 +1) (1+1)^-1 F=4 P=F(1+1) F (1 +1) P=4 [(1+1N1 i(1+1). V N = log(4) log(1+1) i A=F ( (1+1)-1 Depreciation - (Initial Cost - Residual Value) x -1 Interest on Capital - Initial Cost x interest i(1+1) A=P (1+1)-1